
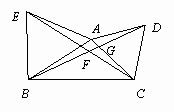
如图,以△ABC的边AB、AC向外作等边△ABE和△ACD,连接BD、CE,线段CE和BD有什么数量关系?证明你的结论;能否求出∠DFC的度数?
|
因为△ ABE和△ACD是等边三角形所以∠ DAC=∠EAB=60°,AE=AB,AD=AC所以∠ EAC=∠DAB在△ AEC和△ABD中
所以△ AEC≌△ABD所以∠ BDA=∠ACE又∠ CGF=∠DGA所以∠ DFC=∠DAC=60°. |
| 经过分析可以发现只需要证明线段BD和CE所在的△AEC和△ABD全等即可,根据等边三角形的性质可以得到AC=AD,AE=AB,∠DAC=∠EAB=60°,进而得到∠EAC=∠BAD,根据SAS得到△AEC≌△ABD,于是结论成立;根据可以得到∠BDA=∠ACE,又∠CGF=∠DGA(对顶角),可以得到∠DFC=60°,问题解决. |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
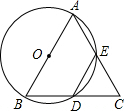 如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE | BD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.
(2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.查看答案和解析>>
科目:初中数学 来源: 题型:
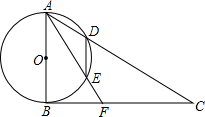 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com