
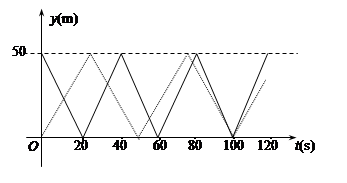
 和
和 时,y关于t的函数关系式:
时,y关于t的函数关系式: ,y= ;当
,y= ;当 时,y= ;
时,y= ;


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
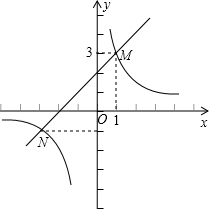
 与直线
与直线 交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程
交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程 的解为
的解为| A.-3,1 | B.-3,3 | C.-1,1 | D.-1,3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,
, 是任意两个不等实数,我们规定:满足不等式
是任意两个不等实数,我们规定:满足不等式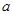 ≤
≤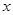 ≤
≤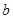 的实数
的实数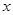 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为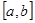 . 对于一个函数,如果它的自变量
. 对于一个函数,如果它的自变量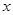 与函数值
与函数值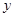 满足:当m≤
满足:当m≤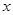 ≤n时,有m≤
≤n时,有m≤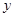 ≤n,我们就称此函数是闭区间
≤n,我们就称此函数是闭区间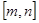 上的“闭函数”.
上的“闭函数”.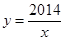 是闭区间
是闭区间 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由; 是闭区间
是闭区间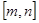 上的“闭函数”,求此函数的表达式;
上的“闭函数”,求此函数的表达式;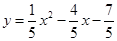 是闭区间
是闭区间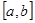 上的“闭函数”,直接写出实数
上的“闭函数”,直接写出实数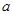 ,
,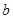 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 随着所处深度
随着所处深度 的变化而变化,在某个地点
的变化而变化,在某个地点 与
与 的关系可以由公式
的关系可以由公式 来表示,则
来表示,则 随
随 的增大1而( )
的增大1而( )| A.增大35 | B.减小 35 | C.不变 | D.以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象如图所示,下列结论正确的是
的图象如图所示,下列结论正确的是| A.它们的函数值y随着x的增大而增大 |
| B.它们的函数值y随着x的增大而减小 |
| C.k<0 |
| D.它们的自变量x的取值为全体实数 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com