
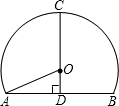
 如图,是一个隧道的截面,如果路面AB宽为8米,净高CD为8米,那么这个隧道所在圆的半径OA是________米.
如图,是一个隧道的截面,如果路面AB宽为8米,净高CD为8米,那么这个隧道所在圆的半径OA是________米.科目:初中数学 来源:2006年福建省泉州市初中毕业、升学考试数学试题 题型:044
一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD.

(1)当AD=4米时,求隧道截面上半圆O的面积;
(2)已知矩形ABCD相邻两边之和为8米,半圆O的半径为r米.
①求隧道截面的面积S(米2)关于半径r(米)的函数关系式(不要求写出r的取值范围);
②若2米≤CD≤3米,利用函数图象求隧道截面的S的最大值(π取3.14,结果精确到0.1米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com