

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:单选题
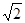 ,则此三角形移动的距离A A'是( )
,则此三角形移动的距离A A'是( )
A.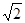 -1 -1 | B.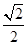 | C.1 | D.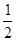 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知) ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( ) AD‖EG,( )
AD‖EG,( ) ∠1=∠2,( )
∠1=∠2,( )  ∠E=∠1(已知)
∠E=∠1(已知) = (等量代换)
= (等量代换)  AD平分∠BAC( )
AD平分∠BAC( )查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
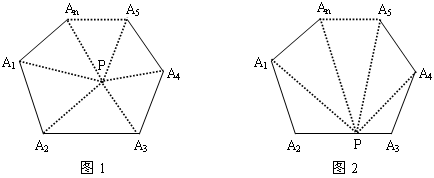
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
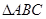 中,
中,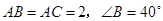 ,点
,点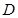 在线段
在线段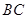 上运动(D不与B、C重合),连接AD,作
上运动(D不与B、C重合),连接AD,作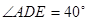 ,
,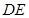 交线段
交线段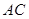 于
于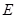
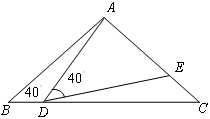
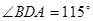 时,
时, °,
°, °;点D从B向C运动时,
°;点D从B向C运动时,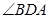 逐渐变 (填“大”或“小”);
逐渐变 (填“大”或“小”);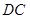 等于多少时,
等于多少时,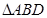 ≌
≌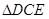 ,请说明理由;s
,请说明理由;s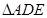 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出 的度数.若不可以,请说明理由。
的度数.若不可以,请说明理由。查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
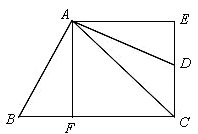
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com