【题目】某件商品的标价是110元，按标价的八折销售时，仍可获利10%，则这件商品每件的进价为_____元．
科目：初中数学 来源： 题型：
【题目】【问题提出】
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”) 和直角三角形全等的判定方法(即“HL”) 后, 我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
不妨将问题用符号语言表示为: 在△ABC和△DEF中, AC = DF, BC = EF, ∠B =∠E,
然后, 对∠B进行分类, 可分为“∠B是直角、钝角、锐角”三种情况进行探究.
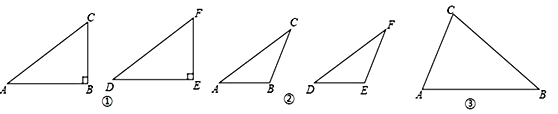
【深入探究】
第一种情况: 当∠B是直角时, △ABC≌△DEF.
(1) 如图①, 在△ABC和△DEF, AC = DF, BC = EF, ∠B =∠E = 90°, 根据_____________, 可以知道Rt△ABC≌Rt△DEF.
第二种情况: 当∠B是钝角时, △ABC≌△DEF.
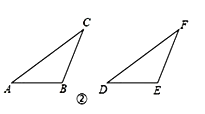
(2) 如图②, 在△ABC和△DEF, AC = DF, BC = EF, ∠B =∠E, 且∠B、∠E都是钝角.
求证: △ABC≌△DEF.
第三种情况: 当∠B是锐角时, △ABC和△DEF不一定全等.
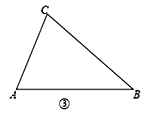
(3) 在△ABC和△DEF, AC = DF, BC = EF, ∠B = ∠E, 且∠B、∠E都是锐角, 请你用尺规在图③中作出△DEF, 使△DEF和△ABC不全等. (不写作法, 保留作图痕迹)
(4) ∠B还要满足什么条件, 就可以使△ABC≌△DEF ? 请直接写出结论: 在△ABC和△DEF中, AC = DF, BC = EF, ∠B =∠E, 且∠B、∠E都是锐角, 若__________, 则△ABC≌△DEF.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，正方形OABC的顶点O与原点重合，顶点A，C分别在x轴、y轴上，反比例函数y=
（k≠0，x＞0）的图象与正方形的两边AB、BC分别交于点M、N，连接OM、ON、MN．
（1）证明△OCN≌△OAM；
（2）若∠NOM=45°，MN=2，求点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列方程的变形中,移项正确的是( )
A. 由7+x=3得x=3+7 B. 由5x=x-3得5x+x=-3
C. 由2x+3-x=7得2x+x=7-3 D. 由2x-7+x=6得2x+x=6+7
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算
（1）（﹣2）﹣2﹣（ 
）0+（﹣ 
）2
（2）am+1a+（﹣a）2am（m是整数）
（3）（x﹣y）（x+y）﹣（x﹣y）2
（4）（x﹣1）（x2﹣1）（x+1）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
