
如图,已知直线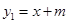 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,与双曲线
,与双曲线
 分别交于点
分别交于点 ,且
,且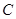 点的坐标为
点的坐标为 .
.
(1)分别求出直线 及双曲线的解析式;
及双曲线的解析式;
(2)求出点 的坐标;
的坐标;
(3)利用图象直接写出:当 在什么范围内取值时,
在什么范围内取值时,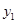 >
> .
.
(1)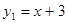 ,
,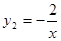 ;(2)D(-2,1);(3)
;(2)D(-2,1);(3)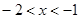
解析试题分析:(1)由点C(-1,2)在直线 及双曲线上即可根据待定系数法求解即可;
及双曲线上即可根据待定系数法求解即可;
(2)把(1)中求得的两个解析式组成方程组求解即可;
(3)找到一次函数的图象在反比例函数的的图象上方的部分对应的x值的取值范围即可得到结果.
解:(1)∵C(-1,2)在双曲线 上,
上,
∴k="-2" ,即双曲线解析式为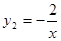
∵C(-1,2)在直线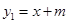 上,
上,
∴2=-1+m,m=3
∴直线解析式为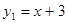 ;
;
(2)由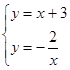 解得
解得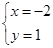 或
或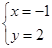
∴点D(-2,1);
(3)当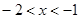 时,
时,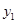 >
> .
.
考点:一次函数与反比例函数的交点问题
点评:一次函数与反比例函数的交点问题是初中数学的重点,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
如图,一次函数 与反比例函数
与反比例函数 的图象相交于点A,且点A的纵坐标为1.
的图象相交于点A,且点A的纵坐标为1.
(1)求反比例函数的解析式;
(2)根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数 (k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(1)求一次函数的解析式;
(2)求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
漳州三宝之一“水仙花”畅销全球,某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
| | A地 | B地 | C地 |
| 运费(元/件) | 20 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com