����������1���ı���PCQD��ƽ���ı��Σ����Խ���PQ��DC��ȣ����ı���PCQD�Ǿ��Σ�Ȼ�����þ��ε����ʣ���PB=x���ɵ÷���x
2+3
2+��2-x��
2+1=8�����б�ʽ����0����֪�˷�����ʵ���������Խ���PQ��DC�ij���������ȣ�
����2����ƽ���ı���PCQD�У���Խ���PQ��DC�ཻ�ڵ�G���ɵ�G��DC���е㣬����Q��QH��BC����BC���ӳ�����H����֤��Rt��ADP��Rt��HCQ���������BH=4����ɵõ�PQ��ABʱ��PQ�ij���С����Ϊ4��
����3����PQ��DC�ཻ�ڵ�G��PE��CQ��PD=DE���ɵ�
=
=
����֤��Rt��ADP��Rt��HCQ���̶����BH�ij���������ô𰸣�
����4����QH��CD����CB���ӳ�����H������C��CK��CD����QH���ӳ�����K����֤��
==
���ADP�ס�BHQ�����ɡ�DCB=45�㣬�ɵá�CKH�ǵ���ֱ�������Σ��̶������CK��ֵ��������ô𰸣�
���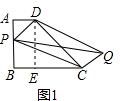
�⣺����1������D��DE��BC�ڵ�E��
������ABCD��AD��BC��AB��BC
���ı���ABED�Ǿ��Σ�
��DE=AB=2��BE=AD=1��
��CE=BC-BE=2��
��DC=2
��
���ı���PCQD��ƽ���ı��Σ�
���Խ���PQ��DC��ȣ����ı���PCQD�Ǿ��Σ�
��PB=x����AP=2-x��
��Rt��DPC��PD
2+PC
2=DC
2����x
2+3
2+��2-x��
2+1=8��
�����x
2-2x+3=0��
�ߡ�=��-2��
2-4��1��3=-8��0��
����⣬
��Խ���PQ��DC��������ȣ�
����2����ͼ2����ƽ���ı���PCQD�У���Խ���PQ��DC�ཻ�ڵ�G��
��G��DC���е㣬
����Q��QH��BC����BC���ӳ�����H��
��AD��BC��
���ADC=��DCH������ADP+��PDG=��DCQ+��QCH��
��PD��CQ��
���PDC=��DCQ��
���ADP=��QCH��
�֡�PD=CQ��
��Rt��ADP��Rt��HCQ��
��AD=HC��
��AD=1��BC=3��
��BH=4��
�൱PQ��ABʱ��PQ�ij���С����Ϊ4��
����3����ͼ2�䣬��PQ��DC�ཻ�ڵ�G��
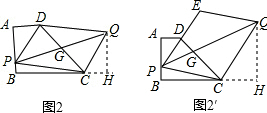
��PE��CQ��PD=DE��
��
=
=
��
��G��DC��һ���㣬
��QH��BC����BC���ӳ�����H��
ͬ����֤��ADP=��QCH��
��Rt��ADP��Rt��HCQ��
��
=
=
��
��CH=2��
��BH=BC+CH=3+2=5��
�൱PQ��ABʱ��PQ�ij���С����Ϊ5��
����4����ͼ3����PQ��AB�ཻ�ڵ�G��
��PE��BQ��AE=nPA��
��
==
��
��G��AB��һ���㣬
��QH��CD����CB���ӳ�����H������C��CK��CD����QH���ӳ�����K��
��AD��BC��AB��BC��
���D=��QHC����DAP+��PAG=��QBH+��QBG=90�㣬��PAG=��QBG��
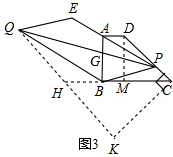
���QBH=��PAD��
���ADP�ס�BHQ��
��
==��
��AD=1��
��BH=n+1��
��CH=BH+BC=3+n+1=n+4��
����D��DM��BC��M��
���ı���ABMD�Ǿ��Σ�
��BM=AD=1��DM=AB=2
��CM=BC-BM=3-1=2=DM��
���DCM=45�㣬
���KCH=45�㣬
��CK=CH•cos45��=
��n+4����
�൱PQ��CDʱ��PQ�ij���С����СֵΪ
��n+4����


 �⣺����1������D��DE��BC�ڵ�E��
�⣺����1������D��DE��BC�ڵ�E��



 ȫ��������ϵ�д�
ȫ��������ϵ�д�
 ��AO��������BO�������4km/h���ٶ���ʻ��th����M�㣬�ҵ���N�㣮
��AO��������BO�������4km/h���ٶ���ʻ��th����M�㣬�ҵ���N�㣮