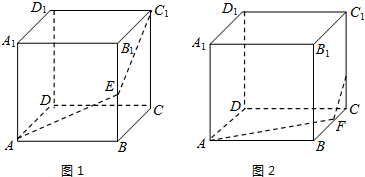
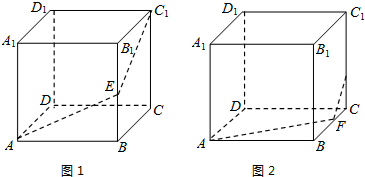
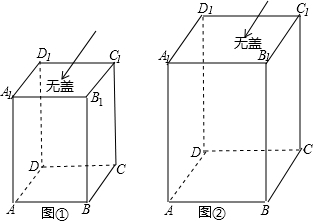
解:根据长方形的对称性,昆虫乙从顶点A沿内壁爬行到昆虫甲C
1处的最短路程有3种可能,
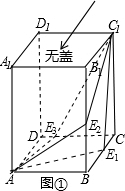
(1)如图①中,图a,A→E
1→C
1,
AE
1C
1=
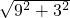
=
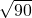
cm,
图b,A→E
2→C
1,
AE
2C
1=
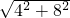
=
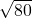
cm,
图c,A→E
3→C
1,
AE
3C
1=
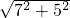
=
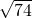
cm,
∵AE
1C
1>AE
2C
1>AE
3C
1,
∴最短路程为
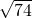
cm,
∴最短路径为A→E
3→C
1,
画法:由△ABE
3∽△ACC
1,
得出:

=

,
∴
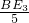
=

,
∴BE
3=2

cm,即取BE
3=2

cm,连接AE
3,E
3C
1即可.
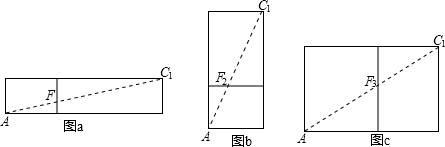
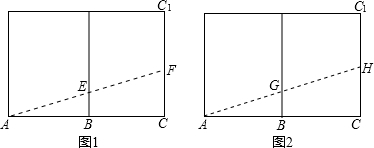
(2)因为昆虫是在侧面上爬行,可以看出,下面两图的最短路径相等,
设昆虫甲从顶点C
1沿棱C
1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F,
爬行捕捉到昆虫甲需x秒钟,如图1在Rt△ACF中,
(3x)
2=12
2+(14-x)
2,
∵x>0,解得:x=5.
答:昆虫乙至少需要5秒钟才能捕捉到昆虫甲.
分析:(1)根据图a,A→E
1→C
1,图b,A→E
2→C
1,以及图c,A→E
3→C
1,利用勾股定理分别求出,即可得出最短路径,画法根据△ABE
3∽△ACC
1,得出BE
3的长度,连接AE
3,E
3C
1即可.
(2)利用昆虫是在侧面上爬行,两种爬行路线的最短路径相等,利用勾股定理求出即可.
点评:此题主要考查了平面展开-最短路径问题以及三角形的相似等知识,立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决,最短路径问题利用平面展开图分别求出是解决问题的关键.

 到昆虫甲?
到昆虫甲?
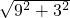 =
=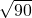 cm,
cm,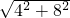 =
=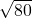 cm,
cm,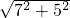 =
=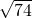 cm,
cm,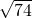 cm,
cm,
 =
= ,
,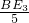 =
= ,
, cm,即取BE3=2
cm,即取BE3=2 cm,连接AE3,E3C1即可.
cm,连接AE3,E3C1即可.


 阅读快车系列答案
阅读快车系列答案