
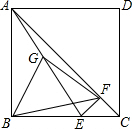
 在正方形ABCD中.
在正方形ABCD中.分析 (1)先根据在直角三角形中,斜边上的中线等于斜边的一半,得出GF=GB,再根据正方形的性质以及三角形外角性质,求得∠BGF=2∠BAF=90°,即可得出△BGF为等腰直角三角形;
(2)分两种情况进行讨论:当E在CB延长线上时,当E在BC延长线上时,分别根据(1)中的方法进行证明即可.
解答  解:(1)证明:∵EF⊥AC于点F,
解:(1)证明:∵EF⊥AC于点F,
∴∠AFE=90°
∵G为斜边AE的中点,
∴在Rt△AEF中,GF=$\frac{1}{2}$AE=AG,
∴∠GAB=∠GBA,
∵∠ABE=90°,G为斜边AE的中点,
∴在Rt△ABE中,BG=$\frac{1}{2}$AE=AG,
∴∠GAF=∠GFA,且GF=GB,
∵∠BGE是△ABG的外角,∠EGF是△AGF的外角,
∴∠BGF=∠BGE+∠EGF=2∠GAB+2∠GAF=2∠BAF=90°,
∴△BGF为等腰直角三角形;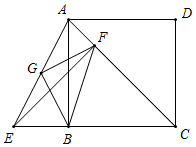
(2)分两种情况:
①如图所示,当E在CB延长线上时,
∵EF⊥AC于点F,
∴∠AFE=90°
∵G为斜边AE的中点,
∴在Rt△AEF中,GF=$\frac{1}{2}$AE=AG,
∴∠GAB=∠GBA,
∵∠ABE=90°,G为斜边AE的中点,
∴在Rt△ABE中,BG=$\frac{1}{2}$AE=AG,
∴∠GAF=∠GFA,且GF=GB,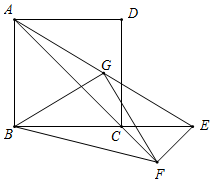
∵∠BGE是△ABG的外角,∠EGF是△AGF的外角,
∴∠BGF=∠EGF-∠BGE=2∠GAF-2∠GAB=2∠BAF=90°,
∴△BGF为等腰直角三角形;
②如图所示,当E在BC延长线上时,
同理可得GF=GB,
∵∠BGE是△ABG的外角,∠EGF是△AGF的外角,
∴∠BGF=∠BGE-∠EGF=2∠GAB-2∠GAF=2∠BAF=90°,
∴△BGF为等腰直角三角形.
点评 本题主要考查了正方形的性质,等腰直角三角形的判定与性质,直角三角形的性质以及三角形外角性质的综合应用,解决问题的关键是掌握:直角三角形中,斜边上的中线等于斜边的一半.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
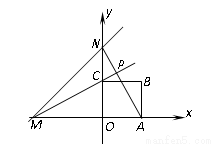
直线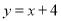 分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
A.  B.
B. 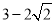 C.
C. 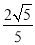 D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为1m/s,则这个人运动到点M所用时间是3s.
如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为1m/s,则这个人运动到点M所用时间是3s.查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
已知a2+3a=1,则代数式2a2+6a-1的值为( )
A. 1 B. 2 C. 3 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
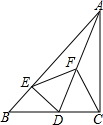 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°
一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com