练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．若代数式x+2的值为1，则x等于（　　）
    A．1B．-1C．3D．-3

    分析 根据题意列出方程，求出方程的解即可得到x的值．

    解答 解：根据题意得：x+2=1，
    解得：x=-1，
    故选B

    点评 此题考查了解一元一次方程方程，根据题意列出方程是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．某校要求八年级同学在课外活动中，必须在五项球类（篮球、足球、排球、羽毛球、乒乓球）活动中任选一项（只能选一项）参加训练，为了了解八年级学生参加球类活动的整体情况，现以八年级2班作为样本，对该班学生参加球类活动的情况进行统计，并绘制了如图所示的不完整统计表和扇形统计图：

    八年级2班参加球类活动人数统计表 
    项目 篮球 足球 乒乓球  排球 羽毛球
     人数a  65  7 6
    根据图中提供的信息，解答下列问题：
    （1）a=16，b=17.5；
    （2）该校八年级学生共有600人，则该年级参加足球活动的人数约90人；
    （3）该班参加乒乓球活动的5位同学中，有3位男同学（A，B，C）和2位女同学（D，E），现准备从中选取两名同学组成双打组合，用树状图或列表法求恰好选出一男一女组成混合双打组合的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）3$\sqrt{3}$+2$\sqrt{8}$-$\sqrt{18}$-$\sqrt{48}$；  
    （2）${（\sqrt{4\frac{1}{2}}-\frac{1}{{\sqrt{2}}}）^2}+\sqrt{12}$；
    （3）$\frac{{\sqrt{9}}}{{\sqrt{12}}}÷\frac{{\sqrt{3}}}{6}×2\sqrt{\frac{2}{3}}$；       
    （4）$（\sqrt{27}+2\sqrt{5}）（\sqrt{20}-3\sqrt{3}）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（　　）
    A．a＞0B．c＜0
    C．3是方程ax2+bx+c=0的一个根D．当x＜1时，y随x的增大而减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．若关于x的一元二次方程x2-3x+p=0（p≠0）的两个不相等的实数根分别为a和b，且a2-ab+b2=18，则$\frac{a}{b}$+$\frac{b}{a}$的值是（　　）
    A．3B．-3C．5D．-5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．若二次函数y=x2+mx的对称轴是x=3，则关于x的方程x2+mx=7的解为（　　）
    A．x1=0，x2=6B．x1=1，x2=7C．x1=1，x2=-7D．x1=-1，x2=7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，已知△ABC，∠BAC=90°，请用尺规过点A作一条直线，使其将△ABC分成两个相似的三角形（保留作图痕迹，不写作法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

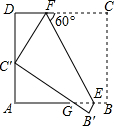    3．如图，正方形ABCD的边长为3，E、F分别是AB、CD上的点，且∠CFE=60°，将四边形BCFE沿EF翻折，得到B′C′FE，C′恰好落在AD边上，B′C′交AB于点G，则GE的长是（　　）
    A．3$\sqrt{3}$-4B．4$\sqrt{2}$-5C．4-2$\sqrt{3}$D．5-2$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．在0，1，-2，3这四个数中，最小的数是（　　）
    A．0B．1C．-2D．3

    查看答案和解析>>

    同步练习册答案