Question

已知M是Rt△ABC中斜边BC的中点，P、Q分别在AB、AC上，且PM⊥QM．求证：PQ²=PB²+QC²．

Answer 1

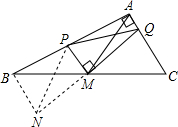
证明：如图，以M点为中心，△MCQ顺时针旋转180°至△MBN，
∴△MCQ≌△MBN，
∴BN=QC，MN=MQ，∠MBN=∠C，
连接PN，∵PM⊥QM，
∴PM垂直平分NQ，
∴PN=PQ，
∵△ABC是直角三角形，BC是斜边，
∴∠ABC+∠C=90°，
∴∠ABC+∠MBN=90°，
即△PBN是直角三角形，
根据勾股定理可得，PN²=PB²+BN²，
∴PQ²=PB²+QC²．
分析：以M点为中心，△MCQ顺时针旋转180°至△MBN，根据旋转的旋转可得△MCQ与△MBN全等，根据全等三角形对应边相等可得BN=QC，MN=MQ，全等三角形对应角相等可得，∠MBN=∠C，再连接PN，可以证明PM垂直平分NQ，所以PN=PQ，然后证明△PBN为直角三角形，根据勾股定理即可证明．
点评：本题考查了直角三角形的旋转，旋转变换的旋转，勾股定理的应用，利用旋转变换把构造出以PQ、PB、QC转化为同一个直角三角形的三边是证明的关键．