
分析 (1)原不等式组变形后由其解集根据“同大取大”可得m的范围;
(2)将x、y的值代入后求得a的值,根据绝对值性质化简原式.
解答 解:(1)原不等式组变形为$\left\{\begin{array}{l}{x>2}\\{x>m+1}\end{array}\right.$,
∵不等式组的解集为x>2,
∴m+1≤2,即m≤1;
(2)∵$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$是方程2x-3=ay的一组解,
∴2-3=-a,解得:a=1,
∴原式=|1-m|-|m-2|
=1-m-(2-m)
=1-m-2+m
=-1.
点评 本题主要考查一元一次不等式组的解集和方程的解及绝对值性质,熟练掌握不等式组解集的确定原则和方程的解得概念、绝对值性质是关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
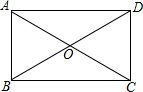 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
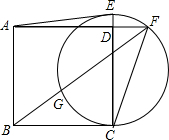 如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
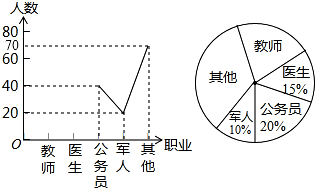
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com