
| x | … | 60 | 65 | 70 | 75 | 80 | … |
| y | … | 60 | 55 | 50 | 45 | 40 | … |
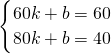 ,
,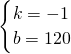 ,
, )2+
)2+ ,当a<0,二次函数有最大值,即x=-
,当a<0,二次函数有最大值,即x=- 时,y的最大值为
时,y的最大值为 ,然后利用二次函数的性质解决有关问题.也考查了待定系数法求函数的解析式以及一次函数的应用.
,然后利用二次函数的性质解决有关问题.也考查了待定系数法求函数的解析式以及一次函数的应用. 

科目:初中数学 来源: 题型:
| 售价(元/件) | … | 55 | 60 | 70 | … |
| 销量(件) | … | 75 | 70 | 60 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
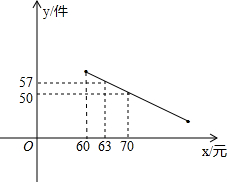 (2012•鄂尔多斯)某商场试销一种成本为每件60元的T恤,规定试销期间销售单价不低于成本单价,且获利不得高于40%.经试销发现,销售量y(件)与销售单价x(元)之间的函数图象如图所示:
(2012•鄂尔多斯)某商场试销一种成本为每件60元的T恤,规定试销期间销售单价不低于成本单价,且获利不得高于40%.经试销发现,销售量y(件)与销售单价x(元)之间的函数图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com