
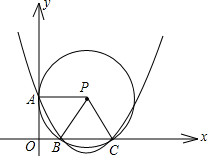
 (2012•海珠区一模)如图,在直角坐标系xOy中,已知点P(2,
(2012•海珠区一模)如图,在直角坐标系xOy中,已知点P(2,| 3 |
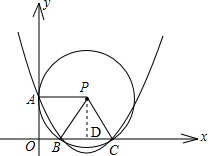 解:(1)过P作PD⊥BC交BC于D,
解:(1)过P作PD⊥BC交BC于D,| 3 |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| BD |
| BP |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
|
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
|
|
| 3 |
| 3 |
| 3 |


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•海珠区一模)在某市初中学业水平考试体育学科的800米耐力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.则下列说法正确的是( )
(2012•海珠区一模)在某市初中学业水平考试体育学科的800米耐力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.则下列说法正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com