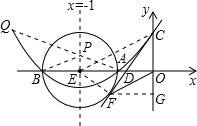
解:(1)∵⊙E的半径为2,
∴点E的坐标为(-4,0)易知A(-2,0),B(-6,0)
∵抛物线过点A和B,
∴
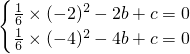
解得
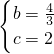
∴抛物线的解析式为y=

x
2+

x+2;
(2)∵抛物线y=

x
2+

x+2与y轴交于点C,
令x=0,y=

×0
2+

×0+2=2,
∴C(0,2)
作图象如右;(未作图的给3分)
(3)∵Q(m,

),
∴

=

m
2+

m+2
整理为m
2+8m-20=0,
即m
1=2,m
2=-10
∵m<0,则m=-10
∴Q(-10,

)
∵y=

(x+4)
2-

,
又∵A(-2,0)与B(-6,0)
关于x=-4对称,则PQ+PB的最小值就是QA的长度
∴PQ+PB=PA+PQ=QA=
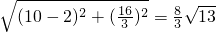
;
(4)解法一:连接EF,
∵EF=2,在Rt△COD与Rt△EFD中,EF=CO=2
又∵∠CDO=∠EDF,
∴Rt△COD≌Rt△EFD
设OD=-x,则ED=CD=4+x,在Rt△COD中2
2+(-x)
2=(4+x)
2,则X
F=-1.5
∴CD=4-1.5=2.5,设∠OCD=∠1,则sin∠1=
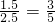
.
设X
1=α
又∵CF=
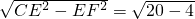
=4,
∴

=sin∠1,
∴
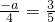
∴a=-

=-2.4
又S
△COF=S
△COM,
∵CO=CO,三角形同底则只要高相等,则S
△COF=S
△COM
∴x
M=X
F或X
M=-X
F,
故存在x
M1=2.4或x
M2=-2.4
y
M1=

×-2.4
2+

x-2.4+2=-0.24,
y
M2=

×2.4
2+

×2.4+2=6.16
∴M的坐标为M
1(-2.4,-0.24),M
2(2.4,6.16)
解法二:如图过F点作y轴的垂线交y轴于G点,由△COD≌△EFD?CD=ED
设OD=xED=CD=4-x,
则有(4-x)
2-x
2=2
2?x=1.5又CF=
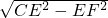
=4
又∵Rt△COD≌Rt△EFD,CD=DE,OD=DF
∴
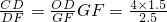
=2.4
若S
△COF=S
△COM,故M点到底边CO的高为2.4,则存在x
M1=2.4或x
M2=-2.4
当x
M1=-2.4时,y
M1=

×(-2.4)
2+

×(-2.4)+2=-0.24,
∴M
1(-2.4,-0.24)x
M2=2.4时,
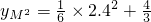
×2.4+2=6.16,
∴M
2(2.4,6.16)
如果有其它不同解法,可依据解法一或解法二的得分标准给分.
分析:(1)根据题意可得点A,B的坐标,将点A,B的坐标代入二次函数的解析式即可求得;
(2)抛物线与y轴的交点横坐标为0,代入求得纵坐标,可得点C的坐标,求得顶点坐标,对称轴即可画草图;
(3)根据两点之间线段最短可得:Q(m,

),∴

=

m
2+

m+2整理为m
2+8m-20=0,即m
1=2,m
2=-10.因m<0,则m=-10,∴Q(-10,

).∵y=

(x+4)
2-

,又∵A(-2,0)与B(-6,0)关于x=-4对称,则PQ+PB的最小值就是QA的长度,求解即可;
(4)根据全等的知识,利用三角函数,借助于方程求解即可.
点评:此题考查了圆与二次函数的综合知识,是中考中难度较大的题目;解题时要注意审题,理解题意;特别是要注意数形结合思想与方程思想的应用.

 x2+bx+c过点A和点B,与y轴交于C点.
x2+bx+c过点A和点B,与y轴交于C点. (1)求抛物线的解析式;
(1)求抛物线的解析式; )(m<0)在抛物线y=
)(m<0)在抛物线y= x2+bx+c的图象上,点P为此抛物线对称轴上的一个动点,求PQ+PB的最小值;
x2+bx+c的图象上,点P为此抛物线对称轴上的一个动点,求PQ+PB的最小值; 解:(1)∵⊙E的半径为2,
解:(1)∵⊙E的半径为2,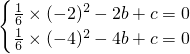
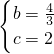
 x2+
x2+ x+2;
x+2; x2+
x2+ x+2与y轴交于点C,
x+2与y轴交于点C, ×02+
×02+ ×0+2=2,
×0+2=2, ),
), =
= m2+
m2+ m+2
m+2 )
) (x+4)2-
(x+4)2- ,
,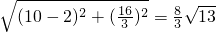 ;
;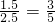 .
.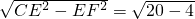 =4,
=4, =sin∠1,
=sin∠1,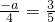
 =-2.4
=-2.4 ×-2.42+
×-2.42+ x-2.4+2=-0.24,
x-2.4+2=-0.24, ×2.42+
×2.42+ ×2.4+2=6.16
×2.4+2=6.16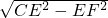 =4
=4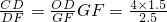 =2.4
=2.4 ×(-2.4)2+
×(-2.4)2+ ×(-2.4)+2=-0.24,
×(-2.4)+2=-0.24,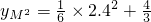 ×2.4+2=6.16,
×2.4+2=6.16, ),∴
),∴ =
= m2+
m2+ m+2整理为m2+8m-20=0,即m1=2,m2=-10.因m<0,则m=-10,∴Q(-10,
m+2整理为m2+8m-20=0,即m1=2,m2=-10.因m<0,则m=-10,∴Q(-10, ).∵y=
).∵y= (x+4)2-
(x+4)2- ,又∵A(-2,0)与B(-6,0)关于x=-4对称,则PQ+PB的最小值就是QA的长度,求解即可;
,又∵A(-2,0)与B(-6,0)关于x=-4对称,则PQ+PB的最小值就是QA的长度,求解即可;

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2