Question

如图，△ABC内接于⊙O，AB是直径，过点A作直线MN，若∠MAC=∠ABC．
（1）求证：MN是⊙O的切线；
（2）设D是弧AC的中点，连接BD交AC于点G，过点D作DE⊥AB于点E，交AC于点F．
①求证：FD=FG；
②若BC=4，AB=6，试求AE的长．

Answer 1

（1）证明：∵AB是直径，
∴∠ACB=90°，
∴∠CAB+∠ABC=90°．
∵∠MAC=∠ABC，
∴∠MAC+∠CAB=90°，即MA⊥AB，
∴MN是⊙O的切线．

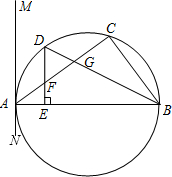
（2）①证明：∵D是弧AC的中点，
∴∠DBC=∠ABD，
∵AB是直径，
∴∠CBG+∠CGB=90°；
∵DE⊥AB，
∴∠FDG+∠ABD=90°，
∵∠DBC=∠ABD，
∴∠FDG=∠CGB=∠FGD，
∴FD=FG．

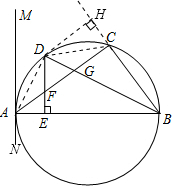
②解：连接AD、CD，作DH⊥BC，交BC的延长线于H点．
∵∠DBC=∠ABD，DH⊥BC，DE⊥AB，
∴DE=DH．
∴△BDE≌△BDH．
∴BE=BH．
∵D是弧AC的中点，
∴AD=DC．
∴Rt△ADE≌Rt△CDH．
∴AE=CH．
∴BE=AB-AE=BC+CH=BH，即6-AE=4+AE，
∴AE=1．
分析：（1）即证∠MAC+∠CAB=90°．因为AB为直径，所以∠ACB=90°，∠ABC+∠CAB=90°．由∠MAC=∠ABC得证．
（2）①证明∠BDE=∠DGF即可．∠BDE=90°-∠ABD；∠DGF=∠CGB=90°-∠CBD．因为D是弧AC的中点，所以∠ABD=∠CBD．问题得证．
②连接AD、CD，作DH⊥BC，交BC的延长线于H点．证明Rt△ADE≌Rt△CDH，得AE=CH．根据AB=BH求解．
点评：此题考查了切线的判定、等腰三角形的判定、三角形全等等知识点，综合性强；特别是最后一个问题构造全等三角形求解，难度较大．