
求证:CF2=CA·AF.

| 作五边形ABCDE的外接圆.
∵ ∠BAC=∠ACB=∠ABF,∴ △ABF∽△ACB. ∴ AF:AB=AB:AC.∴ AB2=CA·AF. 在△CBF中,∠BCF=36°,∠CBF=72°. ∴ ∠BFC=180°-(∠BCF+∠CBF)=72° ∴ CF=CB.又AB=CB,∴ CF=AB.∴ CF2=CA·AF.
|
| 欲证CF2=CA·AF,需证 由于正多边形都有外接圆,故作正五边形的外接圆.这样就为证题提供了宝贵的外在条件.
|


科目:初中数学 来源: 题型:
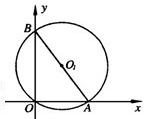 21、已知:如图,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A(3,0)、B(0,4).设△BOA的内切圆的直径为d,求d+AB的值.
21、已知:如图,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A(3,0)、B(0,4).设△BOA的内切圆的直径为d,求d+AB的值.查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 已知:如图,在正五边形ABCDE中,BE分别与AC、AD相交于F、G,下列说法不正确的是
已知:如图,在正五边形ABCDE中,BE分别与AC、AD相交于F、G,下列说法不正确的是查看答案和解析>>
科目:初中数学 来源:2005年江苏省镇江中学高中单独招生考试数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com