
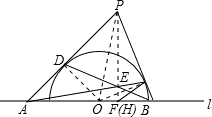
 证明:如图,设AD与BC相交于点P,用O表示半圆T的圆心,
证明:如图,设AD与BC相交于点P,用O表示半圆T的圆心,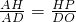 .
. .
.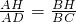 ,从而
,从而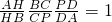 .
.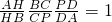 ,即可求证∠DFP=∠DOP=∠COP=∠CFP,即可求证EF平分∠CFD,即可解题.
,即可求证∠DFP=∠DOP=∠COP=∠CFP,即可求证EF平分∠CFD,即可解题.

 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
| 1 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 29、实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.
29、实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 EF的长度为半径画弧,两弧相交于点D;经过点C、D画直线m;则直线CD就是所要求作的垂线.
EF的长度为半径画弧,两弧相交于点D;经过点C、D画直线m;则直线CD就是所要求作的垂线.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
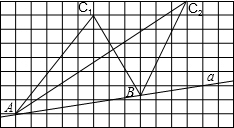 实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.
实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com