
分析 (1)把两个方程的两边分别相加,消去一个未知数y,得到一个一元一次方程.解这个一元一次方程,求得未知数x的值.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数y的值.
(2)用5去乘方程①的两边,使某一个未知数y的系数互为相反数.把两个方程的两边分别相加,消去一个未知数y,得到一个一元一次方程.解这个一元一次方程,求得未知数x的值.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数y的值.
解答 解:(1)$\left\{\begin{array}{l}{x+y=4①}\\{2x-y=5②}\end{array}\right.$
由①+②,可得
3x=9,
解得x=3,
把x=3代入①,可得
3+y=4,
解得y=1,
∴方程组的解为$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+y=3①}\\{3x-5y=11②}\end{array}\right.$
由①×5+②,可得
13x=26,
解得x=2,
把x=2代入①,可得
4+y=3,
解得y=-1,
∴方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 本题主要考查了解二元一次方程组,用加减法解二元一次方程组的一般步骤:①方程组的两个方程中,如果同一个未知数的系数既不相等又不互为相反数,就用适当的数去乘方程的两边,使某一个未知数的系数相等或互为相反数.②把两个方程的两边分别相减或相加,消去一个未知数,得到一个一元一次方程.③解这个一元一次方程,求得未知数的值.④将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数的值.⑤把所求得的两个未知数的值写在一起,就得到原方程组的解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”);
(1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”);查看答案和解析>>
科目:初中数学 来源: 题型:选择题
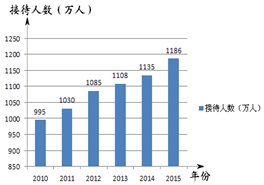 从世妇会NGO论坛到APEC会议、“一带一路”国际峰会,怀柔区正向着积极打造“国际会都”的目标迈进,也吸引着海内外游客到怀柔观光旅游.如图为2010年到2015年我区年接待旅游人数的统计图.
从世妇会NGO论坛到APEC会议、“一带一路”国际峰会,怀柔区正向着积极打造“国际会都”的目标迈进,也吸引着海内外游客到怀柔观光旅游.如图为2010年到2015年我区年接待旅游人数的统计图.| A. | ①③ | B. | ①④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com