A
分析:(1)在等腰三角形中,利用等腰三角形的性质,易证两底角的平分线相等.
(2)在等腰三角形中,利用等边对等角这一性质,通过证全等,易证两腰上的高相等.
(3)若三角形中,有两个外角相等,则其对应的内角相等,所以根据判定定理,有两个外角相等的三角形是等腰三角形.
(4)若有一个角等于60°,另两个角等于30°,90°,则此三角形不是等腰三角形.
解答:(1)∵AB=AC,

∴∠ABC=∠ACB,
∵BE、CD是底角的平分线,
∴∠EBC=∠DCB,
又BC=BC,
∴△DCB≌△ECB,
∴BE=CD,
故等腰三角形两底角的平分线相等.
故(1)正确.
(2)如图
∵CD、BE为高,
∴∠CDB=∠CEB=90°,
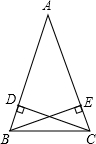
∵AB=AC,
∴∠ABC=∠ACB,
又BC=BC,
∴△DCB≌△ECB,
∴BE=CD,
故等腰三角形两腰的高线相等.
故(2)正确.
(3)若三角形的两个外角相等,故与外角相邻的两个内角相等,根据等腰三角形是判定定理,等角对等边,所是三角形是等腰三角形;
故(3)正确.
(4)若只有一个角等于60°,其他两个角不相等,且不等于60°,所以此三角形不一定是等腰三角形;
故(4)错误.
故选A.
点评:本题主要考查了等腰三角形的性质;做题时,利用性质,通过证三角形全等,来证明等腰三角形中的一些常见结论,应熟记这些结论.




