试题分析:(1)应用思路一:根据条件可以得出BM=CM=MA,由等腰三角形的性质就可以得出∠1=∠B,∠2=∠C,由三角形内角和定理就可以求出结论。
(2)①连接OD,CD,由圆的性质就可以得出AO=OD=OC=a,再由条件就可以得出△ODC是等边三角形,由外角与内角的关系就可以求出∠BDC=30°,从而得出∠ODB=90°而得出结论。
②运用(1)的结论可以得出∠ADB=∠ACE=90°,从而有△ADB∽△AEC,由相似的性质可以得出△ADE∽△ABC,由相似三角形的面积之比等于相似比平方,最后由锐角三角形函数值就可以求出结论。
解:(1)问题研究,应用思路一:
∵M为BC的中点,∴BM=CM=
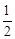
BC。
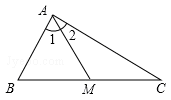
∵MA=
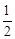
BC,∴BM=CM=MA。
∴∠1=∠B,∠2=∠C。
∵∠1+∠B+∠2+∠C=180°,∴2∠1+2∠2=180°。
∴∠1+∠2=90°,即∠BAC=90°。
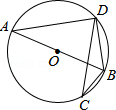
(2)①证明:连接OD,CD,
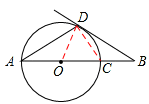
∵∠DAB=30°,OA=a,
∴AO=OD=OC=a,∠BOD=2∠A=60°。
∴△ODC是等边三角形。
∴CD=OC=a,∠DCO=∠CDO=60°。
∵OB=2a,∴BC=a。∴BC=DC。∴∠B=∠BDC。
∴2∠BDC=60°。∴∠BDC=30°。∴∠BDO=∠BDC+∠CDO=90°。
∵OD是⊙O的半径,∴直线BD是⊙O的切线。
②∵M为BC的中点,BD⊥AC于D,∴DM=
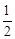
BC。
∵EM=DM,∴EM=
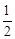
BC。∴∠BEC=90°。∴∠ADB=∠ACE=90°。
∵∠A=∠A,∴△ADB∽△AEC。
∴
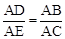
。∴
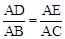
。
∵∠A=∠A,∴△ADE∽△ABC。∴
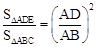
。
∵cos∠A=
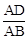
,且∠A=60°,∴
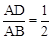
。∴
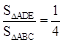
。
∴△ADE与△ABC面积的比值为
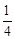
。

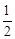 BC,求证∠BAC=90°.
BC,求证∠BAC=90°.
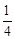 。
。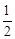 BC。
BC。
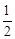 BC,∴BM=CM=MA。
BC,∴BM=CM=MA。
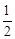 BC。
BC。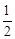 BC。∴∠BEC=90°。∴∠ADB=∠ACE=90°。
BC。∴∠BEC=90°。∴∠ADB=∠ACE=90°。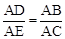 。∴
。∴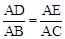 。
。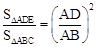 。
。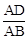 ,且∠A=60°,∴
,且∠A=60°,∴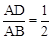 。∴
。∴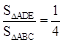 。
。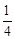 。
。