
 已知△ABC中,∠BAC=120°,AB=AC=4,过点C作直线l∥AB,点D在线段BC上,点E在直线l上,若∠ADE=120°,CE=1,则DC的长为$\sqrt{3}$.
已知△ABC中,∠BAC=120°,AB=AC=4,过点C作直线l∥AB,点D在线段BC上,点E在直线l上,若∠ADE=120°,CE=1,则DC的长为$\sqrt{3}$. 分析 如图,作DM⊥AC于M,DN⊥EC于N.首先证明DM=DN,再证明△ADM≌△EDN,推出AM=EN,DM=DN,设CD=x,列出方程即可解决问题.
解答 解:如图,作DM⊥AC于M,DN⊥EC于N.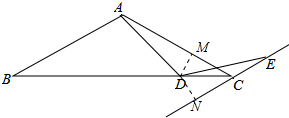
∵∠BAC=120°,AB=AC=4,
∴∠B=∠C=30°,
∵AB∥EN,
∴∠B=∠BCN=30°,
∴∠ACB=∠BCN,
∵DM⊥AC,DN⊥CN,
∴DM=DN,∠CDN=∠CDM=60°,
∴∠ADE=∠MDN=120°,
∴∠ADM=∠EDN,
在△ADM和△EDN中,
$\left\{\begin{array}{l}{∠AMD=∠END=90°}\\{∠ADM=∠EDN}\\{DM=DN}\end{array}\right.$,
∴△ADM≌△EDN,
∴AM=EN,DM=DN,设CD=x,则DM=DN=$\frac{1}{2}$x,CN=CM=$\frac{\sqrt{3}}{2}$x,
∵EN=AM,
∴4-$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{2}$x+1,
∴x=$\sqrt{3}$,
∴CD=$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查角平分线的性质定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用方程的思想去思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国经典数学著作《九章算术》中有这样一道名题,就是“引葭赴岸”问题,(如图)题目是:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”
我国经典数学著作《九章算术》中有这样一道名题,就是“引葭赴岸”问题,(如图)题目是:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com