
 如图正方形的面积为x,圆形的面积为x-2,两个图形的公共部分面积为8,若阴影部分面积为70,则正方形的面积为
如图正方形的面积为x,圆形的面积为x-2,两个图形的公共部分面积为8,若阴影部分面积为70,则正方形的面积为科目:初中数学 来源: 题型:
如图,正方形![]() 的面积为9,点
的面积为9,点![]() 为坐标原点,点
为坐标原点,点![]() 在函数
在函数![]() 的图象上,点
的图象上,点![]() 是函数
是函数![]() 的图象上任意一点,边点
的图象上任意一点,边点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,并设矩形
,并设矩形![]() 和正方形
和正方形![]() 不重合部分的面积为S.
不重合部分的面积为S.

1.⑴求![]() 点的坐标和
点的坐标和![]() 的值;
的值;
2.⑵当![]() 时,求
时,求![]() 点的坐标;
点的坐标;
3.⑶写出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南省长葛市创新中学八年级上学期期末模拟考试数学卷 题型:解答题
如图,正方形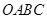 的面积为9,点
的面积为9,点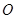 为坐标原点,点
为坐标原点,点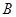 在函数
在函数 的图象上,点
的图象上,点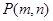 是函数
是函数 的图象上任意一点,边点
的图象上任意一点,边点 分别作
分别作 轴、
轴、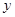 轴的垂线,垂足分别为
轴的垂线,垂足分别为 、
、 ,并设矩形
,并设矩形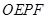 和正方形
和正方形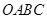 不重合部分的面积为S.
不重合部分的面积为S.
【小题1】⑴求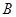 点的坐标和
点的坐标和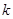 的值;
的值;
【小题2】⑵当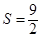 时,求
时,求 点的坐标;
点的坐标;
【小题3】⑶写出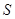 关于
关于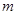 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(内蒙古呼和浩特卷)数学(带解析) 题型:解答题
如图正方形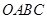 的面积为4,点
的面积为4,点 为坐标原点,点
为坐标原点,点 在函数
在函数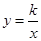 (
(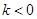 ,
,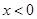 )的图象上,点
)的图象上,点 是函数
是函数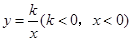 的图象上异于
的图象上异于 的任意一点,过点
的任意一点,过点 分别作
分别作 轴,
轴, 轴的垂线,垂足分别为
轴的垂线,垂足分别为 .
.
(1)设矩形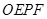 的面积为
的面积为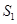 ,判断
,判断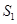 与点
与点 的位置是否有关(不必说理由).
的位置是否有关(不必说理由).
(2)从矩形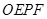 的面积中减去其与正方形
的面积中减去其与正方形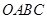 重合的面积,剩余面积记为
重合的面积,剩余面积记为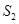 ,写出
,写出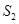 与
与 的函数关系,并标明
的函数关系,并标明 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013届河南省长葛市八年级上学期期末模拟考试数学卷 题型:解答题
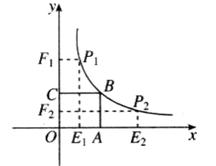
如图,正方形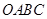 的面积为9,点
的面积为9,点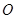 为坐标原点,点
为坐标原点,点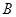 在函数
在函数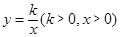 的图象上,点
的图象上,点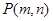 是函数
是函数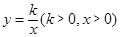 的图象上任意一点,边点
的图象上任意一点,边点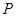 分别作
分别作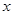 轴、
轴、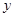 轴的垂线,垂足分别为
轴的垂线,垂足分别为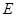 、
、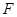 ,并设矩形
,并设矩形 和正方形
和正方形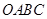 不重合部分的面积为S.
不重合部分的面积为S.
1.⑴求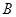 点的坐标和
点的坐标和 的值;
的值;
2.⑵当 时,求
时,求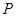 点的坐标;
点的坐标;
3.⑶写出 关于
关于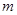 的函数关系式.
的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com