
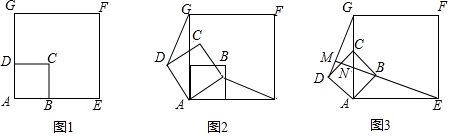
分析 (1)根据正方形的性质得AB=AD,AE=AG,在根据旋转的性质得∠BAE=∠DAG=θ,然后根据“SAS”判断△BAE≌△DAG,则BE=DG;
(2)由BAE≌△DAG得到∠AEB=∠AGD,而∠ANE=∠GNM,根据三角形内角和定理即可得到∠GMN=∠EAN=90°,则EM⊥DG;
(3)连结BD交AG于点H,连结GB,如答图2,由于正方形ABCD绕点A逆时针旋转45°,BD与AC互相垂直平分,且AC在AG上,由AB=3$\sqrt{2}$可得到AH=DH=3,所以GH=7-3=4,然后根据勾股定理可计算出DG=5,则BE=5,解着利用S△DBG=$\frac{1}{2}$BD•GH=$\frac{1}{2}$DG•BM,可计算出BM,所以EM=BM+BE.
解答 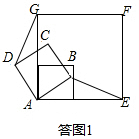 (1)证明:如答图1,∵四边形ABCD,AEFG都是正方形,
(1)证明:如答图1,∵四边形ABCD,AEFG都是正方形,
∴AB=AD,AE=AG,
∵正方形ABCD绕点A逆时针旋转x°(0<x<90),
∴∠BAE=∠DAG=x,
在△BAE和△DAG,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAG}\\{AE=AG}\end{array}\right.$,
∴△BAE≌△DAG(SAS),
∴BE=DG;
(2)证明:∵△BAE≌△DAG,
∴∠AEB=∠AGD,
又∵∠ANE=∠GNM,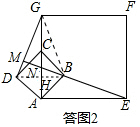
∴∠GMN=∠EAN=90°,
∴EM⊥DG;
(3)解:连结BD交AG于点H,连结GB,如答图2,
∵正方形ABCD绕点A逆时针旋转45°,
∴BD与AC互相垂直平分,且AC在AG上,
∵AB=3$\sqrt{2}$
∴AH=DH=3,
∴GH=7-3=4,
在Rt△GHD中,DG=$\sqrt{D{H}^{2}+G{H}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;
∴BE=5,
∵S△DBG=$\frac{1}{2}$BD•GH=$\frac{1}{2}$DG•BM,
∴BM=$\frac{BD•GH}{DG}$=$\frac{6×4}{5}$=$\frac{24}{5}$,
∴EM=BM+BE=$\frac{24}{5}$+5=9.8.
点评 本题考查了四边形的综合题:熟练掌握正方形的性质和旋转的性质;会运用三角形全等的知识解决线段相等的问题;会运用勾股定理和等腰直角三角形的性质进行几何计算.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:解答题
 在下面过程中的横线上填空,并在括号内注明理由.
在下面过程中的横线上填空,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
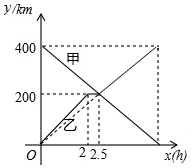 甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km
甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km查看答案和解析>>
科目:初中数学 来源: 题型:解答题
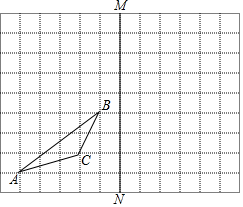 如图,已知三角形ABC和直线MN,且三角形ABC的顶点在网格的交点上.
如图,已知三角形ABC和直线MN,且三角形ABC的顶点在网格的交点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com