
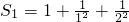 ,
,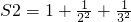 ,
,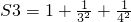 …,
…,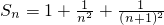 ,设
,设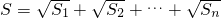 ,其中n为正整数,则用含n的代数式表示S为
,其中n为正整数,则用含n的代数式表示S为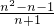

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
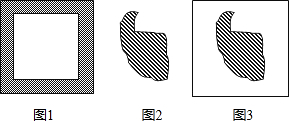
查看答案和解析>>
科目:初中数学 来源: 题型:
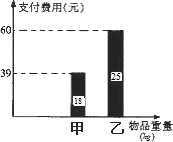 某运输部门规定:办理一件物品的重量不超过akg(a<18)时,需付基础费30元和保险费3元;为限制过重物品的托运,当一件物品的重量超过akg时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某物品的重量为xkg,支付费用为y元.
某运输部门规定:办理一件物品的重量不超过akg(a<18)时,需付基础费30元和保险费3元;为限制过重物品的托运,当一件物品的重量超过akg时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某物品的重量为xkg,支付费用为y元.查看答案和解析>>
科目:初中数学 来源: 题型:

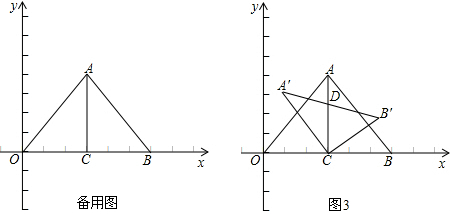
查看答案和解析>>
科目:初中数学 来源: 题型:
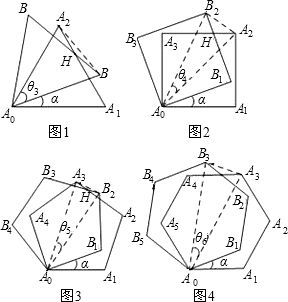
| 180° | n |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| A、2010,510 |
| B、267,4017 |
| C、2010,510,267,4017 |
| D、2008,2006,2004,2002 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com