练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    2012年我市某县筹备20周年县庆，园林部门决定利用现有的3 490盆甲种花卉和2 950盆乙种花卉搭配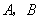两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个种造型需甲种花卉80盆，乙种花卉40盆，搭配一个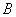种造型需甲种花卉50盆，乙种花卉90盆．

    （1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．

    （2）若搭配一个种造型的成本是800元，搭配一个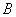种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？


    解：设搭配种造型个，则种造型为个，依题意，得：

     解这个不等式组，得：，.

    是整数，可取，所以可设计三种搭配方案：①种园艺造型个，种园艺造型个；②种园艺造型个，种园艺造型个；③种园艺造型个，种园艺造型个．

    （2）由于种造型的成本高于种造型，所以种造型越少，成本越低，故应选择方案③，成本最低，最低成本为：（元）


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     下列各组图中，由甲图得到乙图，只用平移的方法就能得到的有（　　）

     

    第3题图

    A．1个         B．2个          C．3个          D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    认真阅读下面关于三角形内、外角平分线所夹的探究片段，完成所提出的问题．

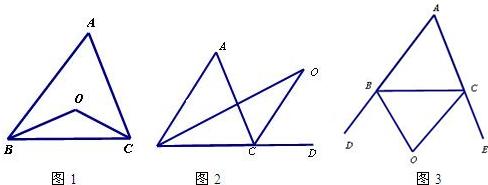
    探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+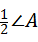，理由如下：

    ∵ BO和CO分别是∠ABC和∠ACB的角平分线，

    ∴.

    ∴ .

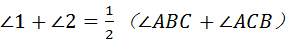    又∵∠ABC+∠ACB=180°﹣∠A，

    ∴ .

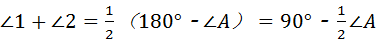    ∴ ∠BOC=180°﹣（∠1+∠2）=180°﹣（90°﹣∠A）

    =.

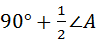    探究2：如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．

    探究3：如图3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）

    结论：　     　．

    第19题图
     
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    当________时，不等式(2－)＜8的解集为＞．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某种商品的进价为800元，出售时标价为1 200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打        折．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知两直线相交，则下列结论成立的是（　　）

    A.所构成的四个角中，有一个角是直角      B.四个角都相等

    C.相邻的两个角互补                      D.对顶角互补

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    等角的余角              ，等角的补角                .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     下列作图属于尺规作图的是（　　）

    A．画线段MN =3 cm

    B．用量角器画出∠AOB 的平分线

    C．用三角尺作过点A垂直于直线l的直线

    D．已知∠α，用没有刻度的直尺和圆规作∠AOB，使∠AOB =2∠α

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    当=－3时，二元一次方程3+5=－3和3－2=+2（关于，的方程）有相同的解，求的值．

    查看答案和解析>>

    同步练习册答案