
 如图,在一张三角形的纸片ABC中,已知∠C=90°,∠A=30°,AB=10.将△ABC纸片折叠后使其中的两个顶点能够互相重合,请画出与说明折痕的各种可能的位置,并求出每条折痕的长.
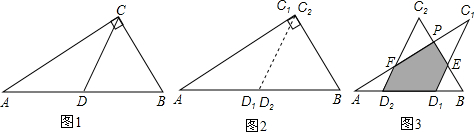
如图,在一张三角形的纸片ABC中,已知∠C=90°,∠A=30°,AB=10.将△ABC纸片折叠后使其中的两个顶点能够互相重合,请画出与说明折痕的各种可能的位置,并求出每条折痕的长. 解:折痕可能位置为△ABC的中位线DE、DF及AB边的垂直平分线DG,如图,
解:折痕可能位置为△ABC的中位线DE、DF及AB边的垂直平分线DG,如图, ,
, BC=
BC= ;
; AC=
AC= ;
; AB=5,∠GDA=90°,
AB=5,∠GDA=90°, DG,
DG, =
= .
. ;然后讨论:当点A与点C重合,折痕为△ABC的中位线DE;当点B与点C重合,折痕为△ABC的中位线DF;当点A与点B重合,折痕为AB的垂直平分线DG,再分别利用三角形的中位线性质和含30度的直角三角形三边的关系即可求出三条折痕的长.
;然后讨论:当点A与点C重合,折痕为△ABC的中位线DE;当点B与点C重合,折痕为△ABC的中位线DF;当点A与点B重合,折痕为AB的垂直平分线DG,再分别利用三角形的中位线性质和含30度的直角三角形三边的关系即可求出三条折痕的长.

科目:初中数学 来源: 题型:
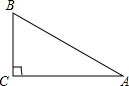 如图,在一张三角形的纸片ABC中,已知∠C=90°,∠A=30°,AB=10.将△ABC纸片折叠后使其中的两个顶点能够互相重合,请画出与说明折痕的各种可能的位置,并求出每条折痕的长.
如图,在一张三角形的纸片ABC中,已知∠C=90°,∠A=30°,AB=10.将△ABC纸片折叠后使其中的两个顶点能够互相重合,请画出与说明折痕的各种可能的位置,并求出每条折痕的长.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
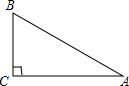
 如图,把一张长方形的纸片ABCD沿BD对折,使C点落在E点处,BE与AD相交于点O,图中除了△ABD≌△CDB外,请写出其他一组全等三角形
如图,把一张长方形的纸片ABCD沿BD对折,使C点落在E点处,BE与AD相交于点O,图中除了△ABD≌△CDB外,请写出其他一组全等三角形查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com