
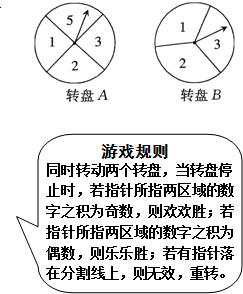
 如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘戏,
如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘戏, 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,直线y=x+b的双曲线y=
如图,直线y=x+b的双曲线y=| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
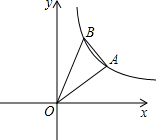 如图所示,Rt△OAB的A,B在反比例函数y=
如图所示,Rt△OAB的A,B在反比例函数y=6
| ||
| x |
A、9
| ||
B、6
| ||
C、12
| ||
D、2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
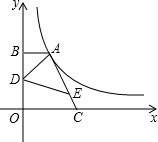 如图,点A在双曲线y=
如图,点A在双曲线y=| k |
| x |
| A、16 | ||
B、
| ||
C、
| ||
| D、9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图为二次函数y=ax2+bx+c的图象,给出下列说法:
如图为二次函数y=ax2+bx+c的图象,给出下列说法:| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.查看答案和解析>>
科目:初中数学 来源: 题型:
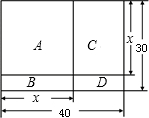 现有一块矩形场地,如图所示,长为40m,宽为30m,要将这块地划分为四块分别种植:A.兰花;B.菊花;C.月季;D.牵牛花.
现有一块矩形场地,如图所示,长为40m,宽为30m,要将这块地划分为四块分别种植:A.兰花;B.菊花;C.月季;D.牵牛花.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com