练习册

  • 练习册
  • 试题
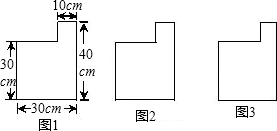
    精英家教网 > 初中数学 > 题目详情

    作一个面积为10cm2的正方形，它的边长可能是


    1. A.
      整数
    2. B.
      分数
    3. C.
      有理数
    4. D.
      无理数
    D
    分析：由于正方形的面积与边长的关系S=a2，由此可求边长．
    解答：∵正方形的面积为10cm2，
    ∴边长=，是无理数．
    故选D．
    点评：本题主要考查了无理数的定义及开平方运算．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，是从边长为40cm、宽为30cm的矩形钢板的左上角截取一块长为20cm、宽为10cm的矩形后，剩下的一块下脚料．工人师傅要将它作适当地切割，重新拼接后焊成一个面积与原下脚料的面积相等，接缝尽可能短的正方形工件．
    （1）请根据上述要求，设计出将这块下脚料适当分割成三块或三块以上的两种不同的拼接方案（在图2和图3中分别画出切割时所沿的虚线，以及拼接后所得到的正方形，保留拼接的痕迹）；
    （2）比较（1）中的两种方案，哪种更好一些？说说你的看法和理由．
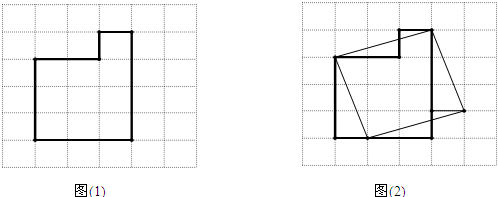
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图（1）是从长40cm、宽30cm的矩形钢板的左上角截取一块长为20cm、宽为10cm的矩形后剩下的一块下脚料．工人师傅要将它作适当切割，重新拼接后焊成一个面积与原下脚料的面积相等，接缝尽可能短的正方形工件．
    精英家教网
    李师傅的做法是：
    设新正方形的边长为x（x＞0）．依题意，割补前后图形的面积相等，有x=
    		302+102
    ．由此可知正方形的边长等于两个直角边分别为30cm和10cm的直角三角形斜边的长．于是，画出如图（2）所示的正方形．
    请你仿照李师傅的做法，确定一个与李师傅方法不同的割补方法，在图（1）的正方形网格图（图中每个小正方形的边长均为10cm）中用虚线画出拼接后的正方形，并在下面的横线上写出接缝的长．（不写分析过程和画法）
    解：接缝的长为
     
     cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

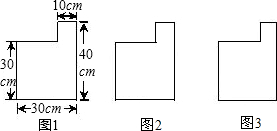    （2012•河西区二模）如图，从边长为40cm、宽为30cm的矩形钢板的左上角截取一块长为20cm，宽为10cm的矩形后，剩下的一块下脚料，工人师傅要将它作适当地切割，重新拼接后焊成一个面积与原下脚料的面积相等，接缝尽可能的正方形工件．
    （1）剩下一块脚料的面积是
    1000cm2
    1000cm2
    ．
    （2）请根据上述要求，设计出将这块下脚料适当分割成三块或三块以上的两种不同的拼接方案（在图2和图3中分别画出切割后所沿虚线，以及拼接后所得到的正方形，保留拼接的痕迹）

    查看答案和解析>>

    科目：初中数学 来源：2012届重庆八中九年级3月月考数学试卷（带解析） 题型：解答题

    如图，梯形ABCD中，BC∥AD,∠ABC=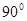,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发，以每秒1cm的速度沿射线BA方向移动，过E作EQ⊥AB,交直线AC于P,交直线BD于Q，以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s，点E的运动时间为t秒.
    （1）求PQ经过O 点时的运动时间t；
    （2）求s与t的函数关系式，并求s的最大值;
    （3）如图（2），若AB的中点为H，DK=1,过H作HT∥AD,交BD于T,交BK于G,求G在正方形PQMN内部时t的取值范围。
      

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年重庆八中九年级3月月考数学试卷（解析版） 题型：解答题

    如图，梯形ABCD中，BC∥AD,∠ABC=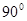,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发，以每秒1cm的速度沿射线BA方向移动，过E作EQ⊥AB,交直线AC于P,交直线BD于Q，以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s，点E的运动时间为t秒.

    （1）求PQ经过O 点时的运动时间t；

    （2）求s与t的函数关系式，并求s的最大值;

    （3）如图（2），若AB的中点为H，DK=1,过H作HT∥AD,交BD于T,交BK于G,求G在正方形PQMN内部时t的取值范围。

     

      

                    

     

    查看答案和解析>>

    同步练习册答案