
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点
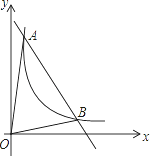
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
【答案】(1)y=﹣2x+8;(2)0<x<1或x>3;(3)8.
【解析】试题分析:(1)、首先根据反比例函数的解析式得出点A和点B的坐标,然后根据待定系数法求出一次函数的解析式;(2)、根据函数图形得出答案;(3)、分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点,将△OAB的面积转化成△OAD的面积减去△OBD的面积.
试题解析:(1)、∵点A(m,6),B(3,n)两点在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1,n=2, 即A(1,6),B(3,2). 又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴![]() . 解得
. 解得![]() , 则该一次函数的解析式为:y=﹣2x+3;
, 则该一次函数的解析式为:y=﹣2x+3;
(2)、根据图象可知使kx+b<![]() 成立的x的取值范围是0<x<1或x>2;
成立的x的取值范围是0<x<1或x>2;
(3)、分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2), 则![]() =4×6÷2-4×2÷2=12-4=8
=4×6÷2-4×2÷2=12-4=8


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】笔记本每本a元,买3本笔记本共支出y元,在这个问题中:
①a是常量时,y是变量;
②a是变量时,y是常量;
③a是变量时,y也是变量;
④a,y可以都是常量或都是变量;
上述判断正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
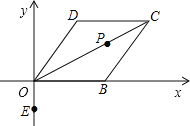
(1)点D的坐标为 ,点C的坐标为 ;
(2)若点P是对角线OC上一动点,点E(0,﹣![]() ),求PE+PB的最小值.
),求PE+PB的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com