练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如图所示，在直角坐标系中，点P是抛物线y=2x2-4x的顶点，此抛物线的对称轴与x轴交于点Q．
    （1）用配方法求此抛物线顶点P的坐标；
    （2）求cos∠POQ的值．

    解：（1）y=2x2-4x=2（x2-2x）
    =2（x2-2x+1）-2
    =2（x-1）2-2．
    因此，抛物线y=2x2-4x的顶点P的坐标是P（1，-2）．

    （2）抛物线y=2x2-4x的对称轴是直线x=1，
    所以此抛物线的对称轴与x轴交于点Q的坐标为Q（1，0）．
    在△OPQ中，∠OQP=90°，OQ=1，PQ=2，
    由勾股定理，得．
    ∴cos∠POQ=．．
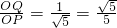    分析：（1）用配方法把y=2x2-4x写成y=a（x+）2+的形式，则顶点P的坐标为（-，）．
    （2）要求cos∠POQ的值，根据余弦函数的定义，只需求出OQ与OP的长度．
    点评：此题考查配方法求二次函数的顶点的坐标，及余弦函数的定义，属于基本题型．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    19、如图所示，在直角坐标系中，矩形OBCD的边长OB=4，OD=2．
    （1）P是OB上一个动点，动点Q在PB或其延长线上运动，OP=PQ，作以PQ为一边的正方形PQRS，点P从O点开始沿线段OB方向运动，直到点P与点B重合，设OP=x，正方形PQRS与矩形OBCD重叠部分的面积为y，写出y与x的函数关系式；
    （2）在（1）中，当x分别取1和3时，y的值分别是多少？
    （3）已知直线l：y=ax-a经过一定点A，求经过定点A且把矩形OBCD的面积平均分成两部分的直线l的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    28、如图所示，在直角坐标系中，矩形OBCD的边长OB=4，OD=2．
    （1）P是OB上一个动点，动点 Q在 PB或其延长线上运动，OP=PQ，作以 PQ为一边的正方形PQRS，点P从O点开始沿射线OB方向运动，直到点P与点B重合，设OP=x，正方形PQRS与矩形OBCD重叠部分的面积为y，写出y与x的函数关系式；
    （2）在（1）中，当x分别取1和3时，y的值分别是多少？
    （3）已知直线l：y=ax-a都经过一定点A，求经过定点A且把矩形OBCD面积平均分成两部分的直线的关系式和A点的坐标．

    查看答案和解析>>

    科目：初中数学 来源：中学学习一本通　数学　七年级下册 北师大课标 题型：044

    已知：如图所示，工人师傅要在墙壁的O处用钻打孔，要使孔口从墙壁对面的B点处打开，墙壁厚是35 cm，B点与O点的铅直距离AB长是20 cm，工人师傅在旁边墙上与AO水平的延长线上截取OC＝35 cm，画CD⊥OC，使CD＝20 cm，联结OD，然后沿着DO的方向打孔，结果钻头正好从B点处打出，你知道这是什么道理吗？你能表达出此题的意思吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图所示，在直角坐标系中，矩形OBCD的边长OB=4，OD=2．
    （1）P是OB上一个动点，动点Q在PB或其延长线上运动，OP=PQ，作以PQ为一边的正方形PQRS，点P从O点开始沿线段OB方向运动，直到点P与点B重合，设OP=x，正方形PQRS与矩形OBCD重叠部分的面积为y，写出y与x的函数关系式；
    （2）在（1）中，当x分别取1和3时，y的值分别是多少？
    （3）已知直线l：y=ax-a经过一定点A，求经过定点A且把矩形OBCD的面积平均分成两部分的直线l的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源：2009年江苏省南通市一中中考数学三模试卷（解析版） 题型：解答题

    如图所示，在直角坐标系中，矩形OBCD的边长OB=4，OD=2．
    （1）P是OB上一个动点，动点Q在PB或其延长线上运动，OP=PQ，作以PQ为一边的正方形PQRS，点P从O点开始沿线段OB方向运动，直到点P与点B重合，设OP=x，正方形PQRS与矩形OBCD重叠部分的面积为y，写出y与x的函数关系式；
    （2）在（1）中，当x分别取1和3时，y的值分别是多少？
    （3）已知直线l：y=ax-a经过一定点A，求经过定点A且把矩形OBCD的面积平均分成两部分的直线l的函数解析式．

    查看答案和解析>>

    同步练习册答案