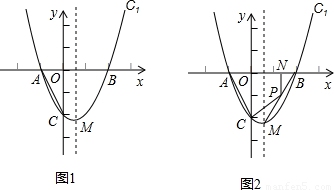
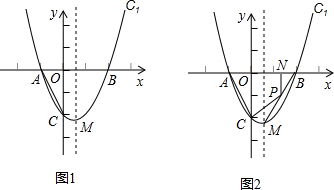
解:(1)根据图形,点A、B关于y轴的对称点分别为(1,0)(-2,0),点C的坐标为(0,-2),
设抛物线C
2的解析式为y=ax
2+bx+c,
则

,
解得

,
所以,抛物线C
2的解析式为y=x
2+x-2;
(2)①AO、CO为一边时,都是以CO、AO为长与宽的矩形,

∵A(-1,0)C(0,-2),
∴AO=1,CO=2,
∴周长为:2(1+2)=2×3=6,
②AC为一边时,根据勾股定理,AC=
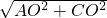
=

=

,
根据三角形的面积,设点O到AC的距离为h,则

×

•h=

×1×2,
解得h=

,
所以,周长为2(

+

)=
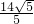
;
(3)根据轴对称与最短距离问题,作点C关于直线BM的对称点C′,过C′作C′N⊥x轴交BM于点P,此时PC+PN最小,
根据对称性,抛物线C
1的解析式为y=x
2-x-2=(x-

)
2-

,
所以,顶点M的坐标为(

,-

),
设直线BM的解析式为y=kx+b,
则

,
解得

,
所以,直线BM的解析式为y=

x-3,
∵直线CC′与直线BM垂直,且经过点C(0,-2),
∴直线CC′的解析式为y=-

x-2,
联立

,
解得

,
∴交点坐标,即CC′的中点坐标为(
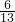
,-
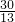
),
根据中点坐标,C′的纵坐标为2×(-
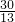
)-(-2)=-

+2=-
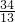
,
∵|-
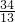
|=
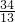
,
∴PC+PN的最小值为
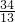
.
分析:(1)根据图象求出点A、B关于y轴的对称点,然后利用待定系数法求二次函数解析式解答即可;
(2)分①AO、CO为一边时,矩形的长与宽分别是CO、AO,然后根据矩形的周长公式列式计算即可得解,②AC为一边时,先根据勾股定理求出AC的长度,再利用三角形的面积求出点O到AC的长度,即为矩形的宽,然后根据矩形的周长公式列式计算即可得解;
(3)作点C关于直线BM的对称点C′,过C′作C′N⊥x轴交BM于点P,此时PC+PN最小,然后对称性求出抛物线C
1的解析式,再求出点M的坐标,然后利用待定系数法求直线解析式求出BM的解析式,再根据互相相垂直的直线的解析式的k值互为负倒数求出直线CC′的解析式,与直线BM的解析式联立求出交点坐标,然后根据中点坐标公式求出点C′的纵坐标,绝对值即为PC+PN的最小值.
点评:本题是对二次函数的综合考查,主要利用了待定系数法求函数解析式,矩形的性质,利用轴对称求最短距离,以及中点坐标公式,(3)中利用互相垂直的直线的解析式的k值互为负倒数求出CC′的直线是解题的关键,也是本题的难点.

 ,
, ,
,
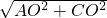 =
= =
= ,
, ×
× •h=
•h= ×1×2,
×1×2, ,
, +
+ )=
)=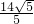 ;
; )2-
)2- ,
, ,-
,- ),
), ,
, ,
, x-3,
x-3, x-2,
x-2, ,
, ,
,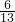 ,-
,-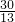 ),
),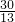 )-(-2)=-
)-(-2)=- +2=-
+2=-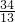 ,
,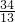 |=
|=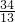 ,
,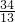 .
.

 字词句段篇系列答案
字词句段篇系列答案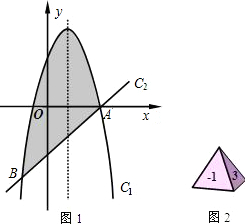 0)和点B.
0)和点B.
 如图,已知抛物线C1的顶点坐标是D(1,4),且经过点C(2,3),又与x轴交于点A、E(点A在点E左边),与y轴交于点B.
如图,已知抛物线C1的顶点坐标是D(1,4),且经过点C(2,3),又与x轴交于点A、E(点A在点E左边),与y轴交于点B.