Question

13．如图1，在平面直角坐标系中，正方形ABCO的顶点C、A分别在x、y轴上，A（0，6）、E（0，2），点H、F分别在边AB、OC上，以H、E、F为顶点作菱形EFGH
（1）当H（-2，6）时，求证：四边形EFGH为正方形
（2）若F（-5，0），求点G的坐标
（3）如图2，点Q为对角线BO上一动点，D为边OA上一点，DQ⊥CQ，点Q从点B出发，沿BO方向移动．若移动的路径长为3，直接写出CD的中点M移动的路径长为$\frac{3\sqrt{2}}{2}$．

Answer 1

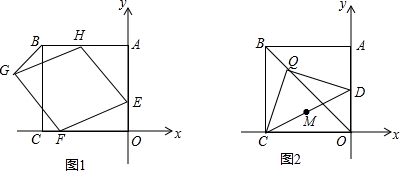
分析 （1）只要证明Rt△AHE≌△Rt△OEF，推出∠AEH=∠EFO，由∠EFO+∠FEO=90°，推出∠AEH+∠FEO=90°，推出∠HEF=90°，即可解决问题．
（2）如图1中，连接GE、FH交于点K．首先求出点H的坐标，设G（m，n），根据中点坐标公式，列出方程组即可解决问题．
（3）如图2中，作MN⊥CO于M．由MN∥OD，CM=MD，推出CN=ON，推出MN垂直平分线段CO，推出点M在线段OC的垂直平分线上运动，如图3中，易知当点Q与B重合时，点M与BD的中点N重合，当BQ=3时，作EQ⊥BC于E，延长EQ交OA于F，延长OM交BC于H，连接NM（线段MN的长即为点M的运动轨迹的长），想办法求出BH的长，即可利用三角形的中位线定理解决问题．

解答 （1）证明：如图1中，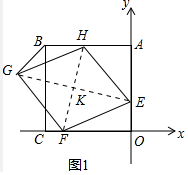

∵E（0，2），H（-2，6），
∴OE=AH=2，
∵四边形ABCO是正方形，
∴∠HAE=∠EOF=90°，
∵四边形EFGH是菱形，
∴EH=EF，
在Rt△AHE和Rt△OEF中，
$\left\{\begin{array}{l}{AH=EO}\\{HE=EF}\end{array}\right.$，
∴Rt△AHE≌△Rt△OEF，
∴∠AEH=∠EFO，
∵∠EFO+∠FEO=90°，
∴∠AEH+∠FEO=90°，
∴∠HEF=90°，
∴四边形EFGH是正方形；

（2）解：如图1中，连接GE、FH交于点K．
∵F（-5，0），E（0，2），
∴OF=5，OE=2，EA=4，
∵HE=EF，
∴5²+2²=4²+AH²，
∴AH=$\sqrt{13}$，
∴H（-$\sqrt{13}$，6），
∵四边形EFGH是菱形，
∴HK=KF，KE=KG，设G（m，n），则有$\frac{m+0}{2}$=$\frac{-5-\sqrt{13}}{2}$，$\frac{n+2}{2}$=$\frac{6+0}{2}$，
∴m=-5-$\sqrt{13}$，n=4，
∴G（-5-$\sqrt{13}$，4）；


（3）解：如图2中，

如图2中，作MN⊥CO于M．
∵MN∥OD，CM=MD，
∴CN=ON，
∴MN垂直平分线段CO，
∴点M在线段OC的垂直平分线上运动，
如图3中，易知当点Q与B重合时，点M与BD的中点N重合，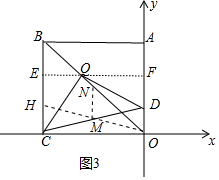

当BQ=3时，作EQ⊥BC于E，延长EQ交OA于F，延长OM交BC于H，连接NM（线段MN的长即为点M的运动轨迹的长），
∵QC=QD，∠CEQ=∠QFD，易证∠ECQ=∠FQD，
∴△EQC≌△FDQ，
∴EQ=DF=BE=$\frac{3\sqrt{2}}{2}$，CE=OF=6-$\frac{3\sqrt{2}}{2}$，
∴DO=6-3$\sqrt{2}$，
∵CM=DM，∠CMH=∠OMD，∠CHM=∠DOM，
∴△HMC≌△OMD，
∴OM=HM，CH=OD=6-3$\sqrt{2}$，BH=3$\sqrt{2}$，
∵ON=NB，
∴MN=$\frac{1}{2}$BH=$\frac{3\sqrt{2}}{2}$，
∴点M的运动的路径的长为$\frac{3\sqrt{2}}{2}$．
故答案为$\frac{3\sqrt{2}}{2}$．

点评 本题考查四边形综合题、正方形的性质、菱形的性质、全等三角形的判定和性质、平行线分线段成比例定理、三角形中位线定理、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造全等三角形解决问题，第三个问题的突破点是证明点M在线段OC的垂直平分线上运动，属于中考压轴题．