
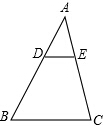
 如图,在△ABC中,已知DE∥BC,AD=2,AB=6,DE=1.5,求:
如图,在△ABC中,已知DE∥BC,AD=2,AB=6,DE=1.5,求:| AE |
| AC |
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
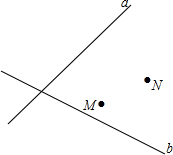 (1)a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留作图痕迹;
(1)a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留作图痕迹;查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
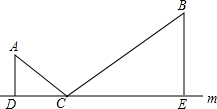 如图,AD⊥m,BE⊥m,垂足分别为D,E.AD=1,BE=2,DE=4,点C为直线上的一个动点,则AC+BC的最小值是( )
如图,AD⊥m,BE⊥m,垂足分别为D,E.AD=1,BE=2,DE=4,点C为直线上的一个动点,则AC+BC的最小值是( )| A、7 | B、5 | C、4.5 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
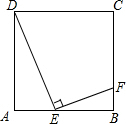 如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F,
如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com