Question

15．在△ABC中，∠BAC=α，边AB的垂直平分线交边BC于点D，边AC的垂直平分线交边BC于点E，连结AD，AE，则∠DAE的度数为2α-180°或180°-2α．（用含α的代数式表示）

Answer 1

分析 分两种情况进行讨论，先根据线段垂直平分线的性质，得到∠B=∠BAD，∠C=∠CAE，进而得到∠BAD+∠CAE=∠B+∠C=180°-α，再根据角的和差关系进行计算即可．

解答 解：分两种情况：
①如图所示，当∠BAC≥90°时，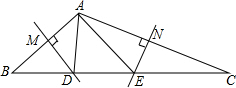

∵DM垂直平分AB，
∴DA=DB，
∴∠B=∠BAD，
同理可得，∠C=∠CAE，
∴∠BAD+∠CAE=∠B+∠C=180°-α，
∴∠DAE=∠BAC-（∠BAD+∠CAE）=α-（180°-α）=2α-180°；
②如图所示，当∠BAC＜90°时，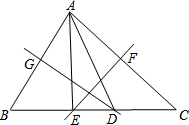

∵DM垂直平分AB，
∴DA=DB，
∴∠B=∠BAD，
同理可得，∠C=∠CAE，
∴∠BAD+∠CAE=∠B+∠C=180°-α，
∴∠DAE=∠BAD+∠CAE-∠BAC=180°-α-α=180°-2α．
故答案为：2α-180°或180°-2α．

点评 本题考查了三角形内角和定理，线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．