
����Ŀ��Ϊ�˽���꼶ѧ��������״����������ijУ���꼶ѧ���������ȡ����ѧ�����а˰��������ܲ��ԣ����Խ����ΪA��B��C��D�ĸ��ȼ������������ͳ��ͼ�е���Ϣ�ش��������⣻
(1)�β��Թ������˶�����ѧ�������ڴ���ϲ�ȫ����ͳ��ͼ��
(2)�����ԣ�ȫ�꼶��4��ѧ�������ر�ã�������1��Ů����ѧУ������4��ѧ������ѡ�����μ��˶��ᣬ�����б�����״ͼ�ķ������Ů����ѡ�еĸ���.
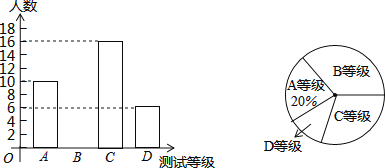
���𰸡�(1)��������50��ѧ������ͼ��������(2)![]() .
.
��������
��1���豾�β��Թ�������![]() ��ѧ�����������塢���塢�ٷֱ�֮��Ĺ�ϵ�г����̼��ɽ��.��������ȥ
��ѧ�����������塢���塢�ٷֱ�֮��Ĺ�ϵ�г����̼��ɽ��.��������ȥ![]() ��
��![]() ��
��![]() �е����������ɽ������������ͼ����.
�е����������ɽ������������ͼ����.
��2������״ͼչʾ����12�ֵȿ��ܵĽ���������ҳ�ǡ�ó鵽��1��Ů���Ľ������Ȼ����ݸ��ʹ�ʽ����.
�⣺(1)�豾�β��Թ�������![]() ��ѧ��.
��ѧ��.
������![]() ��
��
��ã�![]()
�౾�β��Թ�������50��ѧ��.
����Խ��Ϊ![]() �ȼ���ѧ������
�ȼ���ѧ������![]() ��.
��.
����ͳ��ͼ��ͼ��ʾ��

(2)����״ͼ��

����12�ֵȿ��ܵĽ����������ǡ�ó鵽��1��Ů���Ľ����6��
����ǡ�ó鵽��1��Ů���ĸ��ʣ�![]() ��
��![]() .
.


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾2017���ֵ2500��Ԫ��2019���ֵ3025��Ԫ
��1����2017����2019��ù�˾��ֵ����ƽ�������ʣ�
��2���ɣ�1�����ý����Ԥ��2020��ù�˾��ֵ���������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ͼ����ÿ������������Ϊԭ���ĵ�����ԭ����ͼ����������Ϊ0�ĵ���⣩�����겻�䣬���Եõ���һ��������ͼ�����dz��������Ϊ�����任��
���磺��ͼ1����y��x��ͼ�������任��ɵõ�y��![]() ��ͼ���ر�أ���Ϊy��xͼ����������Ϊ0�ĵ���ԭ�㣬���Ըõ㲻���任�����y��
��ͼ���ر�أ���Ϊy��xͼ����������Ϊ0�ĵ���ԭ�㣬���Ըõ㲻���任�����y��![]() ��ͼ����Ҳû��������Ϊ0�ĵ㣮
��ͼ����Ҳû��������Ϊ0�ĵ㣮
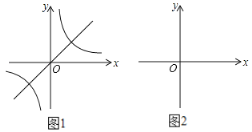
��1������ͼ2�л���y����x��1��ͼ��������������任���ͼ��
��2���۲�����ͼ���ѧ���Ĺ��ں���ͼ������ʵ�֪ʶ��
�ٲ��룺�����任�õ���ͼ���ԭ������ͼ��֮���������������ϵ��д���������ɣ�
��˵�������Ҫ����������һ�����룻
��3����ͼ2�е�ͼ��Ľ���ΪA��B������C������Ϊ����1��m������ABC�����Ϊ6����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר���꾭��ij���ͺŵ�������֪���ͺ������Ľ���Ϊ10��Ԫ/��������һ��ʱ����֣������ͺ������ۼ۶�Ϊ20��Ԫ/��ʱ��ƽ��ÿ���۳�8�����ۼ�ÿ����0.5��Ԫ��ƽ��ÿ�ܶ��۳�1��
��1����ÿ���������ۼ۽���x��Ԫ����ÿ�ܵ����������� �������ú�x�Ĵ���ʽ��ʾ��
��2�����õ�ƻ�ƽ��ÿ�ܵ�����������90��Ԫ��Ϊ�˾�����ٿ�棬�轫ÿ���������ۼ۽��Ͷ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx��1(k��0)�뷴��������y��![]() (m��0)��ͼ���й�����A(1��2)��ֱ��l��x���ڵ�N(3��0)����һ�κ����ͷ�����������ͼ��ֱ��ཻ�ڵ�B��C������AC.
(m��0)��ͼ���й�����A(1��2)��ֱ��l��x���ڵ�N(3��0)����һ�κ����ͷ�����������ͼ��ֱ��ཻ�ڵ�B��C������AC.
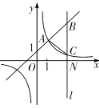
(1)��k��m��ֵ��
(2)���B�����ꣻ
(3)����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����x2+4x+5��y�ύ�ڵ�A����x��������ύ�ڵ�C.
(1)��ֱ��AC����ʽ��
(2)����A��ADƽ����x�ᣬ���������ڵ�D����FΪ�������ϵ�һ��(��F��AD�Ϸ�)����EFƽ����y�ύAC�ڵ�E�����ı���AFDE��������ʱ�����F�����꣬�������������
(3)������P�ȴ�(2)�еĵ�F�������ʵ���·���˶��������߶Գ����ϵ�M�������ش�ֱ��y��ķ����˶���y���ϵĵ�N����Ȼ�����ʵ���·���˶�����Cֹͣ��������P���˶�·�����ʱ�����N�����꣬�������·����.
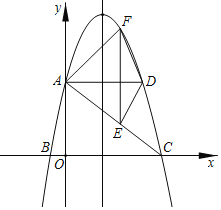
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��3��BC��4����E��AB����һ�㣬��AE��2����F�DZ�BC�ϵ�����һ�㣬�ѡ�BEF��EF���ۣ���B�Ķ�Ӧ��ΪG������AG��CG�����ı���AGCD���������СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��12�·ݣ�����ӭ�����Ҽ��������и��飬Ϊ���˽�ѧ�����������е��˽������ѧУ�����ȡ�˲���ѧ�������ʾ����飬��������������A�dz��˽�![]() �˽�
�˽�![]() �˽����
�˽����![]() ���˽�������ֱ�ͳ�ƣ�����������������ͳ��ͼ(������
���˽�������ֱ�ͳ�ƣ�����������������ͳ��ͼ(������![]() �����ͼ����Ϣ������������⣺
�����ͼ����Ϣ������������⣺
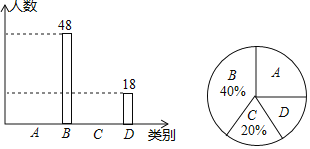
![]() �˴ι�������______��ѧ����
�˴ι�������______��ѧ����
![]() ����ͳ��ͼ��D���ڵ����ε�Բ�Ľ�Ϊ______��
����ͳ��ͼ��D���ڵ����ε�Բ�Ľ�Ϊ______��
![]() ������ͳ��ͼ����������
������ͳ��ͼ����������
![]() ����У����800��ѧ����������ƶ��������е��˽����Ϊ���dz��˽�����ѧ����������
����У����800��ѧ����������ƶ��������е��˽����Ϊ���dz��˽�����ѧ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�ACƽ�֡�DAB����ADC����ACB��90�㣬EΪAB���е㣬
��1����֤��AC2��ABAD��
��2����֤����AFD�ס�CFE��
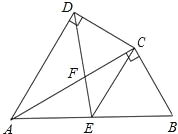
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com