解:(1)AC∥BE;
(2)∠1=∠ABE或∠1=∠DBE;
(3)是真命题,理由如下:
因为BE是△ABC的外角平分线,
所以∠ABE=∠DBE,
又∵∠ABD是三角形ABC的外角,
所以∠ABD=∠1+∠2,
即∠ABE+∠DBE=∠1+∠2,
又∵∠ABE=∠DBE,∠1=∠2,
所以∠ABE=∠1
所以AC∥BE
分析:(1)-(2)要使BE是△ABC的外角平分线,结合三角形的外角的性质∠ABD=∠1+∠2,∠ABE=∠DBE,∠1=∠2,即可证明∠ABE=∠1=∠DBE=∠2,进一步可得BE∥AC;
(3)根据平行线的性质和三角形的外角的性质即可证明.
点评:此题综合运用了角平分线定义、平行线的性质和三角形的外角的性质.

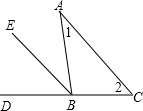 如图,已知在△ABC中,∠1=∠2.
如图,已知在△ABC中,∠1=∠2.
