
| A. | 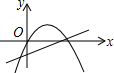 | B. | 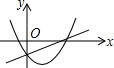 | C. | 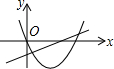 | D. | 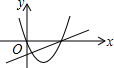 |
分析 本题可先由一次函数y=ax+b图象得到字母系数的正负以及与x轴的交点情况,再与二次函数y=ax2+bx+c的图象相比较看是否一致.
解答 解:A、由抛物线可知,a<0,由直线可知,a>0,故本选项错误;
B、由二次函数y=ax2+bx可知,抛物线经过原点,故本选项错误;
C、由抛物线可知,a>0,x=-$\frac{b}{2a}$>0,得b<0,抛物线与x轴的交点为(0,0),(-$\frac{b}{a}$,0),由直线可知,a>0,b<0,直线与x轴的交点为(-$\frac{b}{a}$,0),故本选项错误;
D、由抛物线可知,a>0,x=-$\frac{b}{2a}$>0,得b<0,抛物线与x轴的交点为(0,0),(-$\frac{b}{a}$,0),由直线可知,a>0,b<0,直线与x轴的交点为(-$\frac{b}{a}$,0),故本选项正确.
故选D.
点评 本本题考查一次函数、二次函数的系数与图象的关系,有一定难度,注意分析简单的函数,得到信息后对照复杂的函数.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
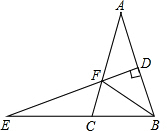 如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.
如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com