
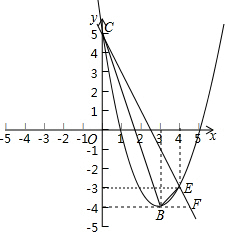 解:(1)设抛物线的解析式为y=a(x-3)2-4,
解:(1)设抛物线的解析式为y=a(x-3)2-4,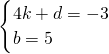 ,
,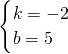 ,
, ×1.5×1=
×1.5×1= ,
, ×9×1.5=
×9×1.5= ,
, -
- =6.
=6.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
 线l2除顶点M不动外仍经过弧A1B1(其余条件不变),那么被雨淋到的几率是扩大了还是缩小了,说明理由.
线l2除顶点M不动外仍经过弧A1B1(其余条件不变),那么被雨淋到的几率是扩大了还是缩小了,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
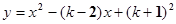
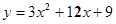 上;
上; 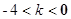 时,抛物线L和x轴有两个不同的交点A、B,求A、B间距取得最大值时k的值;
时,抛物线L和x轴有两个不同的交点A、B,求A、B间距取得最大值时k的值;查看答案和解析>>
科目:初中数学 来源:2013年上海市崇明县中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com