
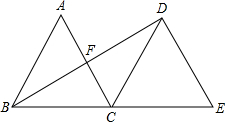
 如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.
如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长. 分析 由平移的性质可知BE=2BC=4,DE=AC=2,故可得出BD⊥DE,由∠E=∠ACB=60°可知AC∥DE,根据勾股定理即可得出BD的长.
解答 解:∵正△ABC沿直线BC向右平移得到正△DCE,
∴BE=2BC=4,BC=CD,DE=AC=2,∠E=∠ACB=∠DCE=∠ABC=60°,
∴∠DBE=$\frac{1}{2}$∠DCE=30°,
∴∠BDE=90°.
在Rt△BDE中,由勾股定理得$BD=\sqrt{B{E^2}-D{E^2}}=\sqrt{{4^2}-{2^2}}=2\sqrt{3}$.
点评 本题考查的是等边三角形的性质及平移的性质,熟知图形平移后的图形与原图形全等的性质是解答此题的关键.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
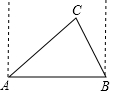 某次军事演习中,有三艘军舰在同一时刻向指挥所报告:A军舰说B军舰在它的正东方向,C军舰在它的北偏东60°方向;B军舰说C军舰在它的北偏西30°方向,C军舰说它到B军舰的距离比它到A军舰的距离近30海里,求A,B军舰的距离?(结果精确到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某次军事演习中,有三艘军舰在同一时刻向指挥所报告:A军舰说B军舰在它的正东方向,C军舰在它的北偏东60°方向;B军舰说C军舰在它的北偏西30°方向,C军舰说它到B军舰的距离比它到A军舰的距离近30海里,求A,B军舰的距离?(结果精确到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.
如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 门票类别 | 散客票 | 团队票A | 团队票B |
| 购票要求 | 超过50人但不超过100人 | 超过100人 | |
| 票价(元/人) | 80元/人 | 70元/人 | 60元/人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
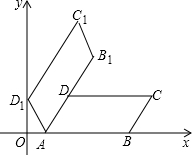 如图,?ABCD的顶点A,B的坐标分别为(1,0),(5,0),∠DAB=60°,AD=2.
如图,?ABCD的顶点A,B的坐标分别为(1,0),(5,0),∠DAB=60°,AD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com