
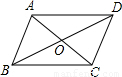
在四边形ABCD中,AC与BD相交于点O,如果只给出条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下六个说法中,正确的说法有( )
(1)如果再加上条件“AD∥BC”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“AB=CD”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“∠DAB=∠DCB”那么四边形ABCD一定是平行四边形;
(4)如果再加上“BC=AD”,那么四边形ABCD一定是平行四边形;
(5)如果再加上条件“AO=CO”,那么四边形ABCD一定是平行四边形;
(6)如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
A.3个 B.4个 C.5个 D.6个
B
【解析】
试题分析:(1)因为两组对边分别平行的四边形是平行四边形,所以①正确;
(2)因为一组对边平行且相等的四边形是平行四边形,所以②正确;
(3)此题易证此四边形的两组对边分别平行,所以③正确;
(5)此题可以通过证明三角形全等,证得AB=CD,所以证得此四边形是平行四边形;正确;
(4)与(6)等腰梯形也符合要求,所以错误.

(1)∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形;正确;
(2)∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形;正确;
(3)∵AB∥CD,
∴∠A+∠D=180°,
∵∠DAB=∠DCB,
∴∠C+∠D=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形;正确;
(4)可能是等腰梯形,所以错误;
(5)∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
∵AO=CO,
∴△AOB≌△COD,
∴AB=CD,
∴四边形ABCD是平行四边形;正确;
(6)此题可以是等腰梯形;错误.
故选B.
考点:本题考查的是平行四边形的判定
点评:解答本题的关键是熟练掌握平行四边形的判定方法:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③对角线互相平分的四边形是平行四边形;
④一组对边平行且相等的四边形是平行四边形.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com