Question

2．如图1，有两个全等的正三角形ABC和ODE，点O、C分别为△ABC、△ODE的重心；固定点O，将△ODE顺时针旋转，使得OD经过点C，如图2所示，则图2中四边形OGCF与△OCH面积的比为（　　）

• A． 1：1
• B． 2：1
• C． 4：1
• D． 4：3

Answer 1

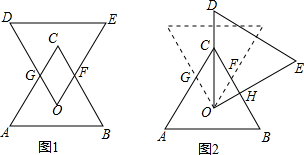
分析 设正三角形的边长是x，则图1中四边形OGCF是一个内角是60°的菱形，图2中△OCH是一个角是30°的直角三角形，分别求得两个图形的面积，即可求解．

解答 解：设正三角形的边长是x，则高长是$\frac{\sqrt{3}}{2}$x．
如图1，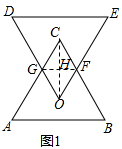

四边形OGCF是一个内角是60°的菱形，OC=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{3}$x．
另一条对角线长是：FG=2GH=2×$\frac{1}{2}$OC•tan30°=2×$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x•tan30°=$\frac{1}{3}$x．
则四边形OGCF的面积是：$\frac{1}{2}$×$\frac{1}{3}$x•$\frac{\sqrt{3}}{3}$x=$\frac{\sqrt{3}}{18}{x}^{2}$；
图2中，OC=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{3}$x．
△OCH是一个角是30°的直角三角形．
则△OCH的面积=$\frac{1}{2}$OC•sin30°•OC•cos30°=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x•×$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{24}{x}^{2}$．
四边形OGCF与△OCH面积的比为：$\frac{\sqrt{3}}{18}{x}^{2}$：$\frac{\sqrt{3}}{24}\\;{x}^{2}$=4：3．
故选：D．

点评 本题主要考查了三角形的重心的性质，解直角三角形，以及菱形、直角三角形面积的计算，正确计算两个图形的面积是解决本题的关键．