
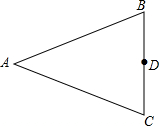
 如图,在△ABC中,AB=AC,D是BC上的任意一点.
如图,在△ABC中,AB=AC,D是BC上的任意一点.分析 (1)作AB与BD的垂线,交于点O,点O就是△ABD的外心,⊙O交线段AC于点E;
(2)连结DE,根据圆内接四边形的性质,等腰三角形的性质,即可得到AD是等腰三角形ABC底边上的高线,从而证明AB是⊙O的直径;
(3)连结BE,根据勾股定理得到关于AE的方程,解方程即可求解.
解答 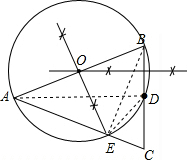 (1)解:如图,⊙O即为所求;
(1)解:如图,⊙O即为所求;
(2)证明:∵过A、B、D三点作⊙O,交线段AC于点E,
∴A、B、D、E四点共圆,
∴∠DEC=∠ABC,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠DEC=∠ACB,
∴DE=CD,
∵$\widehat{DE}$=$\widehat{DB}$,
∴DE=BD,
∴CD=BD,
∴AD⊥BC,
∴AB是⊙O的直径;
(3)解:连结BE,
∵AB是⊙O的直径,
∴BE⊥AC,
由勾股定理可得,AB2-AE2=BC2-(AC-AE)2,即132-AE2=102-(13-AE)2,
解得AE=$\frac{119}{13}$.
故AE的长是$\frac{119}{13}$.
点评 此题考查的是作图-复杂作图,线段垂直平分线的作法,圆内接四边形的性质,等腰三角形的性质,勾股定理,方程思想的应用.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
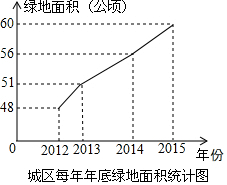 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
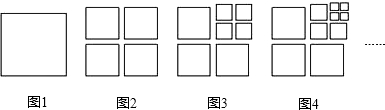
| 图 | 1 | 2 | 3 | 4 | 5 | … |
| 正方形个数 | 1 | 4 | 7 | 10 | 13 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一、三 | B. | 二、四 | C. | 一、四 | D. | 二、三 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
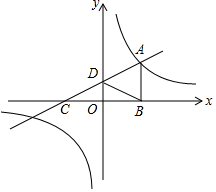 如图,直线y=$\frac{1}{2}$x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点A(m,2),与x轴交于点C,与y轴交于点D,过A作AB⊥x轴于点B,连接BD.
如图,直线y=$\frac{1}{2}$x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点A(m,2),与x轴交于点C,与y轴交于点D,过A作AB⊥x轴于点B,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com