
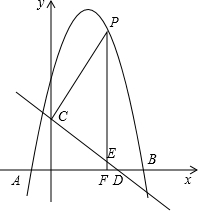
 如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是第一象限内抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是第一象限内抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.分析 (1)利用交点式求抛物线解析式;
(2)先根据坐标轴上点的坐标特征确定C(0,3),D(4,0),则CD=5,设P(m,-m2+4m+5),则E(m,-$\frac{3}{4}$m+3),F(m,0),根据平行线分线段成比例定理,由EF∥OC得到CE:m=5:4,则CE=$\frac{5}{4}$m(0<m<5);
(3)先用m表示PE、PF得到PE=-m2+$\frac{19}{4}$m+2,EF=|-$\frac{3}{4}$x+3|,再利用PE=5EF得到-m2+$\frac{19}{4}$m+2=5|-$\frac{3}{4}$x+3|,然后讨论得到两个关于m的一元二次方程,再解方程求出满足条件的m的值;
(4)作PG∥EC交y轴于G,如图,则四边形PECG为平行四边形,根据菱形的判定,当CE=PE时,四边形PECG为菱形,所以$\frac{5}{4}$m=-m2+$\frac{19}{4}$m+2,然后解方程求出m,从而得到P点坐标.
解答 解:(1)抛物线解析式为y=-(x+1)(x-5),即y=-x2+4x+5;
(2)当x=0时,y=-$\frac{3}{4}$x+3=3,则C(0,3),
当y=0时,-$\frac{3}{4}$x+3=0,解得x=4,则D(4,0),
所以CD=$\sqrt{{3}^{2}+{4}^{2}}$=5,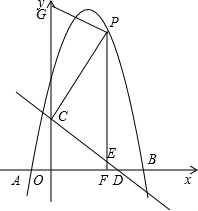
设P(m,-m2+4m+5),则E(m,-$\frac{3}{4}$m+3),F(m,0),
∵EF∥OC,
∴CE:OF=CD:OD,即CE:m=5:4,
∴CE=$\frac{5}{4}$m(0<m<5);
(3)存在.
PE=-m2+4m+5-(-$\frac{3}{4}$m+3)=-m2+$\frac{19}{4}$m+2,EF=|-$\frac{3}{4}$x+3|,
∵PE=5EF,
∴-m2+$\frac{19}{4}$m+2=5|-$\frac{3}{4}$x+3|,
当-m2+$\frac{19}{4}$m+2=5(-$\frac{3}{4}$x+3),解得m1=6.5(舍去),m2=2,
当-m2+$\frac{19}{4}$m+2=-5(-$\frac{3}{4}$x+3),解得m1=$\frac{1-\sqrt{69}}{2}$(舍去),m2=$\frac{1+\sqrt{69}}{2}$,
综上所述,m的值为2或$\frac{1+\sqrt{69}}{2}$;
(4)作PG∥EC交y轴于G,如图,
则四边形PECG为平行四边形,
当CE=PE时,四边形PECG为菱形,
即$\frac{5}{4}$m=-m2+$\frac{19}{4}$m+2,解得m1=$\frac{1}{2}$,m2=4,
此时P点坐标为($\frac{1}{2}$,$\frac{27}{4}$)或(4,5).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、菱形的判定与性质和平行线分线段成比例定理;会利用待定系数法求抛物线解析式;理解坐标与图形性质.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{13}{33}$ | B. | $\frac{104}{63}$ | C. | $\frac{2×13}{3×7}$ | D. | $\frac{23×13}{32×7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,函数y=3x和y=ax+4的图象相交于点A(1,3),则不等式3x≥ax+4的解集为( )
如图,函数y=3x和y=ax+4的图象相交于点A(1,3),则不等式3x≥ax+4的解集为( )| A. | x≥1 | B. | x≤3 | C. | x≤1 | D. | x≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 59 | 96 | 116 | 290 | 480 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.58 | 0.60 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
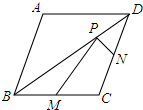 如图,已知菱形ABCD的两条对角线长分别是3和4,点M、N分别是边BC、CD的中点,点P是对角线上的一点,则PM+PN的最小值是$\frac{5}{2}$.
如图,已知菱形ABCD的两条对角线长分别是3和4,点M、N分别是边BC、CD的中点,点P是对角线上的一点,则PM+PN的最小值是$\frac{5}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com