练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    抛物线过点（2，-2）和（-1，10），与x轴交于A、B两点，与y轴交于C点．
    （1）求抛物线的解析式．
    （2）求△ABC的面积．

    (1);（2）6.

    解析试题分析：（1）根据二次函数y=x2+bx+c的图象过点（2，-2）和点（-1，10）两点，把两点坐标代入二次函数解析式，即可求出b、c的值，从而确定抛物线的解析式．
    （2）令y=0,求出A、B两点的横坐标，进而可求△ABC的面积．
    试题解析：（1）把点（2，-2）和（-1，10）代入中，得
     解得
    ∴所求二次函数解析式为．
    （2）在中，令x=0，得y=4．
    ∴C(0，4)．
    令y=0，得，
    解得x=1或x=4．
    ∴A(1，0) ，B(4，0)．
    ∴AB=3，OC=4
    ∴
    考点: 待定系数法求二次函数解析式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    某跳水运动员进行10m跳台跳水的训练时,身体（看成一点）在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线（图中标出的数据为己知条件）．在跳某个规定动作时,正确情况下,该运动员在空中的最高处距水面m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误．

    (l)求这条抛物线的解析式;
    (2)在某次试跳中,测得运动员在空中的运动路线是（1）中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为,问:此次跳水会不会失误?通过计算说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，抛物线过x轴上两点A(9,0),C(-3,0),且与y轴交于点B(0,-12).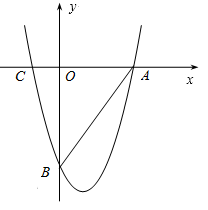

    （1）求抛物线的解析式；
    （2）若动点P从点A出发，以每秒2个单位沿射线AC方向运动；同时，点Q从点B出发，以每秒1个单位沿射线BA方向运动，当点P到达点C处时，两点同时停止运动.问当t为何值时，△APQ∽△AOB？
    （3）若M为线段AB上一个动点，过点M作MN平行于y轴交抛物线于点N．
    ①是否存在这样的点M，使得四边形OMNB恰为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．
    ②当点M运动到何处时，四边形CBNA的面积最大？求出此时点M的坐标及四边形CBNA面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知二次函数的图象经过点（4，3），（3，0）．

    （1）求b、c的值；
    （2）求出该二次函数图象的顶点坐标和对称轴，并在所给坐标系中画出该函数的图象；
    （3）该函数的图像经过怎样的平移得到的图像？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知二次函数图象顶点为C（1,0）,直线与该二次函数交于A,B两点,其中A点（3,4）,B点在y轴上.

    （1）求此二次函数的解析式；
    （2）P为线段AB上一动点（不与A,B重合）,过点P作y轴的平行线与二次函数交于点E.设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式；
    （3）D为线段AB与二次函数对称轴的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形？若存在,请求出P点坐标；若不存在,请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在平面直角坐标系xOy中，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C（0,4），D为OC的中点.

    （1）求m的值；
    （2）抛物线的对称轴与 x轴交于点E，在直线AD上是否存在点F，使得以点A、B、F为顶点的三角形与△ADE 相似？若存在，请求出点F的坐标，若不存在，请说明理由；
    （3）在抛物线的对称轴上是否存在点G，使△GBC中BC边上的高为？若存在，求出点G的坐标；若不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知二次函数.
    （1）求顶点坐标和对称轴方程；
    （2）求该函数图象与x标轴的交点坐标；
    （3）指出x为何值时，；当x为何值时，.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在平面直角坐标系中，抛物线经过点A的坐标为（m，m），点B的坐标为（n，-n），且经过原点O，连接OA、OB、AB，线段AB交y轴于点C．已知实数m，n（m＜n）分别是方程x2-2x-3=0的两根．

    （1）求m，n的值．
    （2）求抛物线的解析式．
    （3）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E两点（点D在y轴右侧），连接OD，BD．当△OPC为等腰三角形时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知抛物线的顶点在x轴上，且与y轴交于A点. 直线经过A、B两点，点B的坐标为（3，4）.
    （1）求抛物线的解析式，并判断点B是否在抛物线上；
    （2）如果点B在抛物线上，P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于点E，设线段PE的长为h，点P的横坐标为x.当x为何值时，h取得最大值，求出这时的h值.

    查看答案和解析>>

    同步练习册答案