
 如图,在直角坐标系中.
如图,在直角坐标系中.分析 (1)在坐标系内描出各点,依次连接各点即可;
(2)连结BD,根据S四边形ABCD=S△ABD+S△CBD即可求得四边形ABCD的面积.
解答 解:(1)如图所示:
(2)连结BD,如图.
∵B(-8,4),D(1,4),
∴BD=9,
∵A(-3,8),C(-3,1),
∴A到BD距离为4,C到BD距离为3,
∴S四边形ABCD=S△ABD+S△CBD
=$\frac{1}{2}$BD•4+$\frac{1}{2}$BD•3
=$\frac{1}{2}$×(4+3)×9
=$\frac{63}{2}$.
点评 本题主要考查坐标与图形性质以及三角形的面积,求不规则图形的面积的方法就是“割”或“补”,即把不规则的图形转化成规则图形的和或差.


科目:初中数学 来源: 题型:选择题
| A. | 了解妫水河的水质情况,选择抽样调查 | |
| B. | 了解某种型号节能灯的使用寿命,选择全面调查 | |
| C. | 了解一架Y-8GX7新型战斗机各零部件的质量,选择抽样调查 | |
| D. | 了解一批药品是否合格,选择全面调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
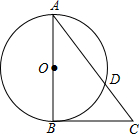 如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.
如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=8,则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=8,则cosB的值是( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的网格中,每个小正方形的边长都为1.
在如图所示的网格中,每个小正方形的边长都为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,P为正方形ABCD的边BC上一动点(点P与点B,C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
如图,P为正方形ABCD的边BC上一动点(点P与点B,C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com