
 当a=5,b=3时,
当a=5,b=3时, 与
与 的大小关系是______.
的大小关系是______. 与
与 的大小关系是______.
的大小关系是______. 与
与 的大小关系是:______.
的大小关系是:______. =
= =4,
=4, =
=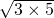 =
= .
. ,
, >
> ;
; =
=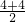 =4,
=4, =
=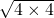 =4,
=4, =
= ;
;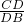 =
=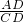 ,即
,即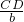 =
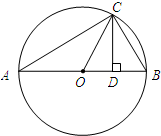
=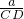 ,CD=
,CD= ,
, AB=
AB= ;
; ,CD=
,CD= ;
; >
> ;
; =
= ;
; ≥
≥ .
. ≥
≥ (当a=b时,取“=”).
(当a=b时,取“=”). 与
与 的大小;
的大小;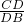 =
=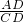 ,代入即可求出CD,求出AB,即可求出OC;
,代入即可求出CD,求出AB,即可求出OC; >
> ,当O和D重合时得出
,当O和D重合时得出 =
= ,即可得出答案
,即可得出答案 ≥
≥ .
.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
 的路程y(km)与时间x(h)的函数图象如图所示.
的路程y(km)与时间x(h)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
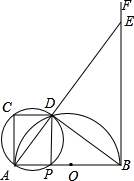 B重合),过A、P、C三点的圆与⊙O相交于除点A以外的另一点D,连接AD并延长交射线BF于点E,连接DB、DP、DC.
B重合),过A、P、C三点的圆与⊙O相交于除点A以外的另一点D,连接AD并延长交射线BF于点E,连接DB、DP、DC.查看答案和解析>>
科目:初中数学 来源: 题型:
 矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿线段DA、线段BA向点A的方向运动,当动点M运动到点A时,M、N两点同时停止运动.连接FM、FN.设点M、N的运动速度都是1个单位/秒,M、N运动的时间为x秒,问:当x为多少时,FM⊥FN?
矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿线段DA、线段BA向点A的方向运动,当动点M运动到点A时,M、N两点同时停止运动.连接FM、FN.设点M、N的运动速度都是1个单位/秒,M、N运动的时间为x秒,问:当x为多少时,FM⊥FN?查看答案和解析>>
科目:初中数学 来源: 题型:
 抛物线上的一点C,使△OCA∽△OBC,且AC:BC=
抛物线上的一点C,使△OCA∽△OBC,且AC:BC=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com