
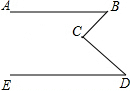
 如图所示,AB∥ED,∠B=48°,∠D=42°,BC垂直于CD吗?如果垂直请说明理由.
如图所示,AB∥ED,∠B=48°,∠D=42°,BC垂直于CD吗?如果垂直请说明理由.  能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:选择题
| A. | 2002年美国在阿富汗的战争中每月耗费10亿美元 | |
| B. | 人的大脑有10000000000个细胞 | |
| C. | 小明买了5本小说 | |
| D. | 有关部门预测,2012年以DVD形式出售的影片将首次超过盒式录像带,达到95亿美元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 捐款(元) | 5 | 10 | 50 | 100 |
| 人数 | 1 | 4 | 3 | 2 |
| A. | 100,50 | B. | 30,10 | C. | 10,10 | D. | 10,50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠D,∠B=∠E,AB=DE | B. | ∠A=∠D,∠B=∠E,AC=DF | ||
| C. | AB=DE,∠B=∠E,BC=EF | D. | AB=DE,∠B=∠E,AC=DF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com