

 ,即
,即 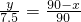 ,
,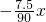 ,
,
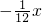 ,
,
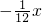 ;
;
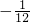 ×30=5(小时).
×30=5(小时).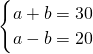 ,
,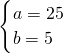 ,
,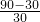 =2小时,此时橡皮艇漂流了10千米.
=2小时,此时橡皮艇漂流了10千米.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
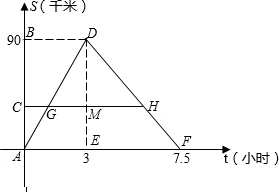
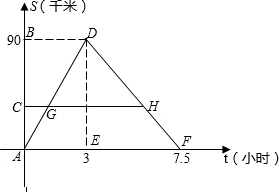
 某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
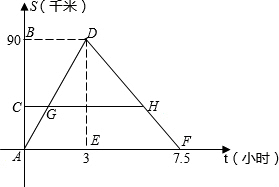 某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市江南中学中考数学一模试卷(解析版) 题型:解答题
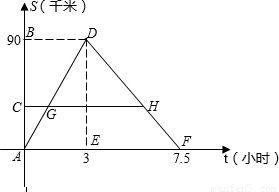
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com