
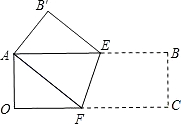
(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.

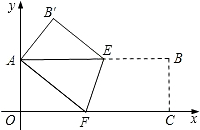
(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.

(1)同意,理由见解析;(2) ,y=3x-12.
,y=3x-12.
【解析】
试题分析:(1)同意.
理由:因为AB∥OC,所以∠AEF=∠EFC.根据折叠性质,有∠AFE=∠EFC.所以∠AEF=∠AFE,AE=AF.△AEF为等腰三角形.
(2)过点E作EG⊥OC于点G.设OF=x,则CF=9-x;由折叠可知:AF=9-x.
在Rt△AOF中,AF2=AO2+OF2 即:32+x2=(9-x)2,解得x=4,AE=AF=9-x=5,FG=OG-OF=5-4=1.在Rt△EFG中,EF2=EG2+FG2=10,求出EF=
设直线EF的解析式为y=kx+b(k≠0),因为点E(5,3)和点F(4,0)在直线EF上,所以,代入解得解得k,b,进而求出解析式.
试题解析:(1)同意.
理由:∵AB∥OC,∴∠AEF=∠EFC.
根据折叠性质,有∠AFE=∠EFC.
∴∠AEF=∠AFE,
∴AE=AF.
∴△AEF为等腰三角形.
(2)过点E作EG⊥OC于点G.
设OF=x,则CF=9-x;
由折叠可知:AF=9-x.
在Rt△AOF中,AF2=AO2+OF2
∴32+x2=(9-x)2,
∴x=4,9-x=5.
∴AE=AF=5,
∴FG=OG-OF=5-4=1.
在Rt△EFG中,
EF2=EG2+FG2=10,
∴EF=
设直线EF的解析式为y=kx+b(k≠0),
∵点E(5,3)和点F(4,0)在直线EF上,
∴3=5k+b,0=4k+b,
解得:k=3,b=-12.
∴y=3x-12.
考点:1.折叠问题.2.一次函数的解析式.3.勾股定理.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
 23、观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.
23、观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分) 1.(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′ 处(如图1),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.(3分)

2.(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.(4+3分)

查看答案和解析>>
科目:初中数学 来源: 题型:
观察与发现:将矩形纸片A![]() OCB折叠,使点C与点A重合,点B落在点B′ 处 (如图1),折痕为EF.小明发现△ AEF为等腰三角形,你同意吗?请说明理由.
OCB折叠,使点C与点A重合,点B落在点B′ 处 (如图1),折痕为EF.小明发现△ AEF为等腰三角形,你同意吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com